��Ŀ����
����Ŀ����ֱ������ϵ�У����Dz����������꣬�������Ϊ�����ĵ��֮Ϊ���й�������
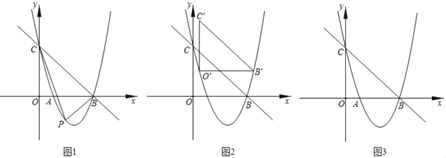
��1������y=![]() x+2��ͼ�����������й����������ꣻ
x+2��ͼ�����������й����������ꣻ
��2������y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й����������������k��ֵ����Ӧ���й����������ꣻ
��k��0��kΪ��������ͼ��������ֻ���������й����������������k��ֵ����Ӧ���й����������ꣻ
��3�������κ���y=![]() ��kΪ��������ͼ����x���ཻ�õ�������ͬ�����й����������ʸú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ�������ж��ٸ����й�������
��kΪ��������ͼ����x���ཻ�õ�������ͬ�����й����������ʸú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ�������ж��ٸ����й�������
���𰸡���1����0,2������2����k=1ʱ����Ӧ���й�����Ϊ��1,1������1����1������k=��1ʱ����Ӧ���й�����Ϊ��1����1��������1,1������3��6��.
��������
���⣨1����Ϊx��������x��0ʱ��![]() x��һ��������������x��0ʱ��
x��һ��������������x��0ʱ��![]() x+2��������������x=0��y=2���ݴ��������y=
x+2��������������x=0��y=2���ݴ��������y=![]() x+2��ͼ�����������й����������꼴�ɣ�
x+2��ͼ�����������й����������꼴�ɣ�
��2�������жϳ���k=1ʱ������y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й���������1��1��������1����1����Ȼ���жϳ���k��1ʱ������y=
��k��0��kΪ��������ͼ��������ֻ���������й���������1��1��������1����1����Ȼ���жϳ���k��1ʱ������y=![]() ��k��0��kΪ��������ͼ����������4�����й��������ݴ��������k��ֵ����Ӧ���й����������꼴�ɣ�
��k��0��kΪ��������ͼ����������4�����й��������ݴ��������k��ֵ����Ӧ���й����������꼴�ɣ�
��3�������k2��3k+2��x2+��2k2��4k+1��x+k2��k=0����[��k��1��x+k][��k��2��x+��k��1��]=0�����x1��x2��ֵ�Ƕ��٣�Ȼ�����x1��x2��ֵ�����������k��ֵ�Ƕ��٣������ݺ����꣬�������Ϊ�����ĵ��֮Ϊ���й��������жϳ��ú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ�������ж��ٸ����й��������ɣ�
�����������1����x��������x��0ʱ��![]() x��һ����������
x��һ����������
��x��0ʱ��![]() x+2����������
x+2����������
��x=0��y=2��
������y=![]() x+2��ͼ�������й������������ǣ�0��2����
x+2��ͼ�������й������������ǣ�0��2����
��2������k=1ʱ������y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й�������
��k��0��kΪ��������ͼ��������ֻ���������й�������
��1��1��������1����1����
����k=��1ʱ������y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й�������
��k��0��kΪ��������ͼ��������ֻ���������й�������
��1����1��������1��1����
����k�١�1ʱ������y=![]() ��k��0��kΪ��������ͼ����������4�����й�������
��k��0��kΪ��������ͼ����������4�����й�������
��1��k��������1����k������k��1��������k����1�������뺯��y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й�����ì�ܣ�
��k��0��kΪ��������ͼ��������ֻ���������й�����ì�ܣ�
���Ͽɵã�k=1ʱ������y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й���������1��1��������1����1����
��k��0��kΪ��������ͼ��������ֻ���������й���������1��1��������1����1����
k=��1ʱ������y=![]() ��k��0��kΪ��������ͼ��������ֻ���������й���������1����1��������1��1����
��k��0��kΪ��������ͼ��������ֻ���������й���������1����1��������1��1����
��3���k2��3k+2��x2+��2k2��4k+1��x+k2��k=0��
��[��k��1��x+k][��k��2��x+��k��1��]=0��
��
��![]() ��
��
�������ɵ�
x1x2+2x2+1=0��
��x2��x1+2��=��1��
��x1��x2����������
��![]() ��
��![]()
��![]() ��
��![]()
����![]() ʱ��
ʱ��
��![]() ��
��
��k=![]() ��
��
����![]() ʱ��
ʱ��
��![]() ��
��
��k=k��1���⣻
���ϣ��ɵ�
k=![]() ��x1=��3��x2=1��
��x1=��3��x2=1��
y=��k2��3k+2��x2+��2k2��4k+1��x+k2��k
=[(![]() )2��3��
)2��3��![]() +2]x2+[2����
+2]x2+[2����![]() ��2��4��
��2��4��![]() +1]x+��
+1]x+��![]() ��2��
��2��![]()
=��![]() x2��
x2��![]() x+
x+![]()
����x=��2ʱ��
y=��![]() x2��
x2��![]() x+
x+![]() =��
=��![]() ������2��2��
������2��2��![]() ������2��+
������2��+![]()
=![]()
����x=��1ʱ��
y=��![]() x2��
x2��![]() x+
x+![]()
=��![]() ������1��2��
������1��2��![]() ������1��+
������1��+![]()
=1
����x=0ʱ��y=![]() ��
��
���⣬�ú�����ͼ����x����Χ�ɵ�ƽ��ͼ����x���ϵ����й�������3����
����2��0��������1��0������0��0����
���ϣ��ɵ�
�����κ���y=��k2��3k+2��x2+��2k2��4k+1��x+k2��k��kΪ��������ͼ����x���ཻ�õ�������ͬ�����й�������
�ú�����ͼ����x����Χ�ɵ�ƽ��ͼ���У����߽磩��һ��������6�����й�����������3��0��������2��0��������1��0������1��1������0��0������1��0����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�