题目内容
【题目】已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
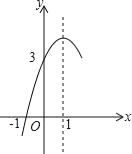
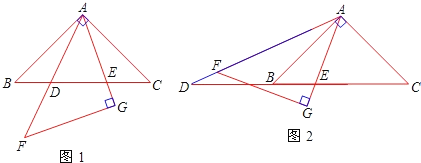
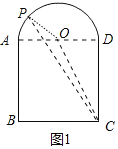
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
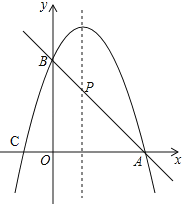
(2)如图2,在平面直角坐标系中,已知点A(﹣1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.
①若d=2,求点C所在的区域的面积;
②若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.
【答案】(1)2;②1+![]() ;(2)①π;②
;(2)①π;②![]() ,
,![]() .
.
【解析】
(1)①根据平面图形S的宽距定义可直接得出答案;②正方形ABCD的边长为2,设半圆的圆心为O,点P是⊙O上一点,连接OP,PC,OC,根据勾股定理可求出OC,从而得到答案;
(2)①如图2-1,点C所在的区域是图中![]() ,面积为
,面积为![]() ;②如图2-2,当点M在y轴的右侧时,连接AM,作MT⊥x轴于T,求出d的值,即可判断,再根据对称性求出点M在y轴左侧的情形即可.
;②如图2-2,当点M在y轴的右侧时,连接AM,作MT⊥x轴于T,求出d的值,即可判断,再根据对称性求出点M在y轴左侧的情形即可.
解:(1)①半径为1的圆的宽距离为2,
故答案为2.
②如图1,正方形ABCD的边长为2,设半圆的圆心为O,点P是⊙O上一点,连接OP,PC,OC.
在Rt△ODC中,![]()
∴OP+OC≥PC,
∴![]() ,
,
∴这个“窗户形“的宽距为![]() .
.
故答案为1+![]() .
.
(2)①如图2﹣1中,点C所在的区域是以AB为直径的圆,因为点A(﹣1,0)、B(1,0),所以此圆的半径为1,所以面积为π.
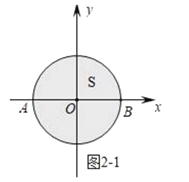
②如图2﹣2中,当点M在y轴的右侧时,连接AM,作MT⊥x轴于T.
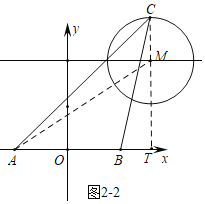
∵AC≤AM+CM,又∵5≤d≤8,
∴当d=5时.AM=5-1=4,MT=2
∴![]() ,此时
,此时![]() ,
,
当d=8时.AM=8-1=7,MT=2
∴![]() ,此时
,此时![]() ,
,
∴满足条件的点M的横坐标的范围为![]() .
.
当点M在y轴的左侧时,满足条件的点M的横坐标的范围为![]() .
.
故答案为![]() ,
,![]() .
.

【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图: A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价 (元/件) | 6 | 5.2 | 6.5 |
B产品单价 (元/件) | 3.5 | 4 | 3 |

并求得了A产品三次单价的平均数和方差:![]() ;
;![]()
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0)使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值。