Question

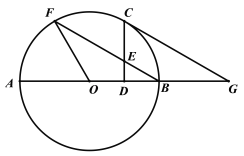
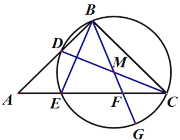
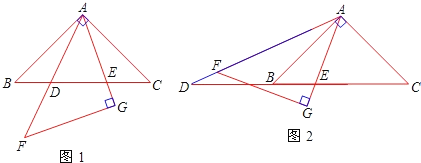
【题目】如图1，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，AB=4.若△ABC固定不动，△AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合，点E不与点C重合).

(1)求证：△ABE∽△DCA；

(2)若BE·CD=k（k为常数），求k的值；

(3)在旋转过程中，当△AFG旋转到如图2的位置时，AG与BC交于点E，AF的延长线与CB的延长线交于点D，那么（2）中k的值是否发生了变化?为什么?

Answer 1

【答案】（1）见解析；（2）k=16；（3）不变，理由见详解.

【解析】

（1）由于∠BAE=∠BAD+45°，∠CDA=∠BAD+45°，那么∠BAE=∠CDA，而∠B=∠C=45°，易证△ABE∽△DCA；
（2）由（1）知△ABE∽△DCA，可得，利用AB=CA=4，可求k的值；

（3）不变．由于∠BEA=∠EAC+45°，∠CAD=45°+∠EAC，易得∠BEA=∠CAD，而∠ABE=∠DCA=45°，可证△EBA∽△ACD，利用比例线段可求BECD=ABAC，而根据题意知AB=CA=4，从而可求k的值，可得不变的结论．

解：（1）∵三角形ABC和三角形AFG是两个全等的等腰直角三角形，

∴∠FAG=∠ACB=45°，∠B=∠C=45°，
∴∠BAE=∠BAD+45°，∠CDA=∠BAD+∠B =∠BAD+45°，
∴∠BAE=∠CDA，
∴△ABE∽△DCA，

（2）由（1）可知△ABE∽△DCA，

∴，

∴

又∵三角形ABC是等腰直角三角形，AB=4，

∴AB=CA=4，

∴，

即，

（3）不变．
∵∠BEA=∠EAC+∠C =∠EAC+45°，

∠CAD=∠FAG +∠EAC=45°+∠EAC
∴∠BEA=∠CAD，
又∵∠ABE=∠DCA=45°，
∴△EBA∽△ACD，

∴，

∴，