题目内容
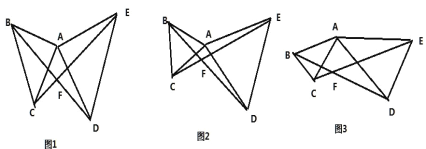
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
【答案】(1)90°;(2)60°;(3)![]() 证明见解析;
证明见解析;
【解析】
(1)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(2)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(3)根据![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(1)如图:
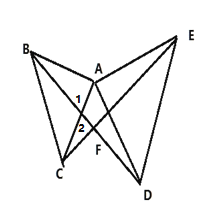
∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
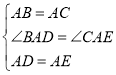 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:90°
(2)如图:
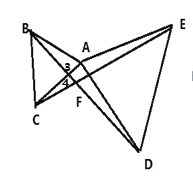
∵△ABC和△ADE都是等边三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
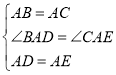 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:60°
(3) ![]() 理由如下:
理由如下:
∵∠BAC=∠DAE
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
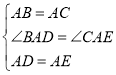 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∴![]()

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目