题目内容
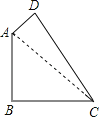
【题目】如图，在四边形ABCD中，AB＝BC＝2，CD＝3，AD＝1，且∠ABC＝90°，连接AC．
（1）求AC的长度．
（2）求证△ACD是直角三角形．
（3）求四边形ABCD的面积？
【答案】（1）2
；（2）见解析；（3）2+
【解析】
（1）利用勾股定理计算即可；
（2）利用勾股定理的逆定理证明即可；
（3）根据四边形ABCD的面积＝S△ABC+S△ACD＝
AB×BC+AD×AC计算即可．
解：（1）在直角△ABC中，AC为斜边，且AB＝BC＝2，则AC＝
＝
＝2．
（2）∵AD＝1，CD＝3，AC＝2
∴AC2+AD2＝CD2，
即△ACD为直角三角形，且∠DAC＝90°，
（3）四边形ABCD的面积＝S△ABC+S△ACD＝AB×BC+AD×AC＝×2×2+×1×2＝2+．
答：四边形ABCD的面积为2+．
练习册系列答案
相关题目
