题目内容
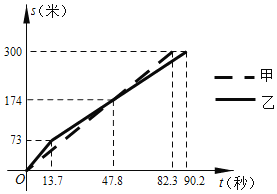
【题目】随着智能手机的普及，“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐，某商场对2019年712月中使用这两种手机支付方式的情况进行统计，得到如图所示的折线图，根据统计图中的信息，得出以下四个推断，其中不合理的是（ ）
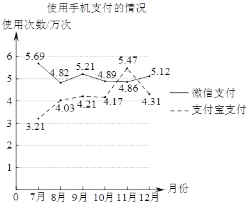
A.6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多；
B.6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大；
C.6个月中11月份使用手机支付的总次数最多；
D.9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多；
【答案】B
【解析】
从折线统计图中得到每个月使用“微信支付”的次数、使用“支付宝支付”的次数，计算后即可判断．
解：A、6个月中使用“微信支付”的总次数=5.69+4.82+5.21+4.89+4.86+5.12=30.59，
6个月中使，“支付宝支付”的总次数=3.21+4.03+4.21+4.17+5.47+4.31=25.4，
∴6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多，本选项说法合理；
B、从统计图中不能得到消费总额的信息，本选项说法不合理；
C、7月份使用手机支付的总次数为5.69+3.21=8.9，
8月份使用手机支付的总次数为4.82+4.03=8.85，
9月份使用手机支付的总次数为5.21+4.21=9.42，
10月份使用手机支付的总次数为4.89+4.17=9.06，
11月份使用手机支付的总次数为4.86+5.47=10.33，
12月份使用手机支付的总次数为5.12+4.31=9.43，
∴6个月中11月份使用手机支付的总次数最多，本选项说法合理；
D、9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多，本选项说法合理；
故选：B．
七星图书口算速算天天练系列答案
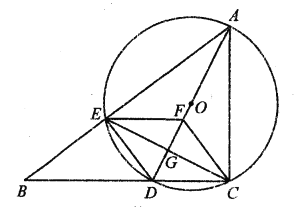
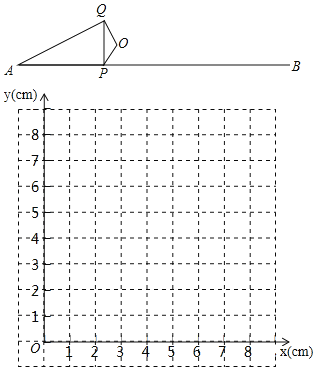
初中学业考试导与练系列答案
【题目】如图，P是线段AB上的一点，AB＝6cm，O是AB外一定点．连接OP，将OP绕点O顺时针旋转120°得OQ，连接PQ，AQ．小明根据学习函数的经验，对线段AP，PQ，AQ的长度之间的关系进行了探究．
下面是小明的探究过程，请补充完整：
（1）对于点P在AB上的不同位置，画图、测量，得到了线段AP，PQ，AQ的长度（单位：cm）的几组值，如表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP，PQ，AQ的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；/span>
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解决问题：当AQ＝PQ时，线段AP的长度约为 cm．
【题目】疫情期间，甲、乙、丙、丁4名同学约定周一至周五每天做一组俯卧撑．为了增加趣味性，他们通过游戏方式确定每个人每天的训练计划．
首先，按如图方式摆放五张卡片，正面标有不同的数字代表每天做俯卧撑的个数，反面标有
，
，
，
，
便于记录．
具体游戏规则如下：
甲同学：同时翻开，，将两个数字进行比较，然后由小到大记录在表格中，，，按原顺序记录在表格中；
乙同学：同时翻开，，，将三个数字进行比较，然后由小到大记录在表格中，，按原顺序记录在表格中；
以此类推，到丁同学时，五张卡片全部翻开，并由小到大记录在表格中．
下表记录的是这四名同学五天的训练计划：
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | |
甲同学 |
|
|
|
|
|
乙同学 |
|
|
|
|
|
丙同学 | |||||
丁同学 |
|
|
|
|
|
根据记录结果解决问题：
（1）补全上表中丙同学的训练计划；
（2）已知每名同学每天至少做30个，五天最多做180个．
①如果
，
，那么所有可能取值为__________________________；
②这四名同学星期_________做俯卧撑的总个数最多，总个数最多为_________个．
