题目内容
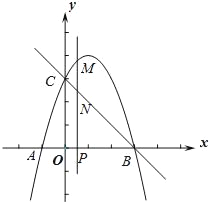
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
【答案】(1) y=﹣x+3;(2)m=2;(3)![]()
【解析】试题分析:
(1)把点A(﹣1,0),点C(0,3)代入抛物线y=﹣x2+bx+c列出方程组求得b、c的值即可得到抛物线的解析式,在所得抛物线的解析式中,由y=0可得关于x的一元二次方程,解方程可求得B的坐标;有B、C的坐标用“待定系数法”可求得直线BC的解析式;
(2)由△CMN是以MN为腰的等腰直角三角形可得,CM∥x轴,由点C的坐标(0,3)可得点M的纵坐标为3,把y=3代入抛物线的解析式解得x的值即可得到m的值;
(3)由已知把M、N的坐标用含“m”的代数式表达出来,进一步表达出MN的长,根据题意可得MN=OC=3即可列出关于“m”的方程,解方程即可求得m的值.
试题解析:
(1)把点A(﹣1,0),点C(0,3)代入抛物线y=﹣x2+bx+c,得![]() ,解得
,解得![]() ,∴抛物线的解析式为y=﹣x2+2x+3;
,∴抛物线的解析式为y=﹣x2+2x+3;
令﹣x2+2x+3=0,解得x1=﹣1,x2=3,
∴点B的坐标(3,0),
设直线BC的解析式为y=kx+b,把C(0,3),B的坐标(3,0)代入,得![]() ,解得:
,解得:![]() ,∴直线BC的解析式为y=﹣x+3.
,∴直线BC的解析式为y=﹣x+3.
(2)∵△CMN是以MN为腰的等腰直角三角形,
∴CM∥x轴,即点M的纵坐标为3,
把y=3代入y=﹣x2+2x+3,得x=0或2,
∵点M不能与点C重合,
∴点P的横坐标为m=2.
(3)∵抛物线的解析式为y=﹣x2+2x+3,P的横坐标为m
∴M(m,﹣m2+2m+3),
∵直线BC的解析式为y=﹣x+3.
∴N(m,﹣m+3),
∵以C、O、M、N为顶点的四边形是以OC为一边的平行四边形,
∴MN=OC=3,
∴﹣m2+2m+3﹣(﹣m+3)=3,化简得m2﹣3m+3=0,无解,
或(﹣m+3)﹣(﹣m2+2m+3)=3,化简得m2﹣3m﹣3=0,
解得m=![]() ,
,
∴当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,m的值为![]() .
.

【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图的统计图(图中信息不完整).已知A,B两组捐款人数的比为1∶5.
捐款人数分组统计表
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
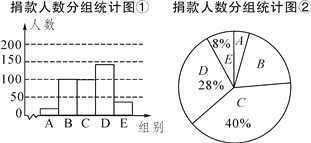
请结合以上信息解答下列问题:
(1)a=____,本次调查的样本容量是______;
(2)先求出C组的人数,再补全“捐款人数分组统计图①;
(3)若该学校自愿捐款的学生有1500人,请估计捐款不少于30元的学生有多少人?