题目内容
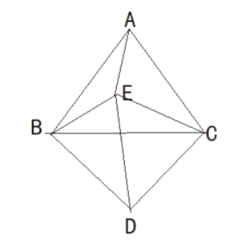
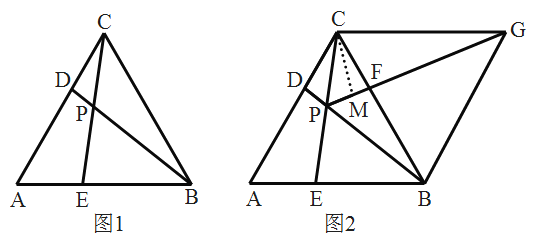
【题目】如图,![]() 是等边三角形,点
是等边三角形,点![]() ,
,![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
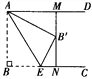
(2)如图2,将![]() 沿直线
沿直线![]() 翻折得到对应的
翻折得到对应的![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
①试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
②若四边形![]() 的面积为
的面积为![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①四边形![]() 为菱形,理由见解析,②CE=3
为菱形,理由见解析,②CE=3
【解析】
(1)根据SAS证明:△ACE≌△CBD;(2)①根据(1)中:△ACE≌△CBD,得∠ACE=∠CBD,则∠DPC=∠ACB=60°,证明△CDB≌△CFG,可得CG=AB=AC,则四边形ABGC是菱形;②作高CH,设菱形ABGC的边长为a,根据菱形的面积列式为:ABCH=6![]() ,即a
,即a![]() a=6
a=6![]() ,可得a的值,证明△BGF∽△PGB,列比例式可得FG的长,由△CDB≌△CFG,△ACE≌△CBD,根据对应边相等可得结论.
,可得a的值,证明△BGF∽△PGB,列比例式可得FG的长,由△CDB≌△CFG,△ACE≌△CBD,根据对应边相等可得结论.
(1)证明:
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() .
.
又![]() ,
,
![]() .
.
(2)解:①四边形![]() 为菱形,理由如下:
为菱形,理由如下:
![]()
![]()
![]()
由翻折可知:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() ,
,
![]() 平行四边形
平行四边形![]() 为菱形.
为菱形.
图2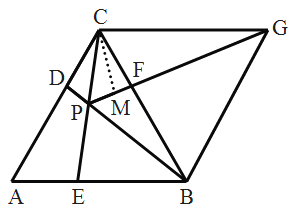
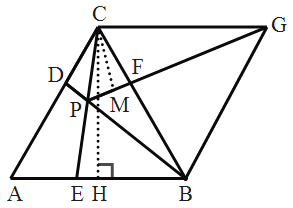
②过![]() 作
作![]() 于点
于点![]() .
.
设菱形![]() 的边长为
的边长为![]() .
.
![]() 为等边三角形,
为等边三角形,
![]()
![]()
![]()
![]() 菱形
菱形![]() 的面积为
的面积为![]() ,
,
![]() ,即
,即![]() .
.
![]()
![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]()
又![]()
![]()
![]() 为公共角,
为公共角,
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
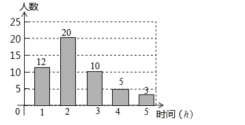
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?