题目内容
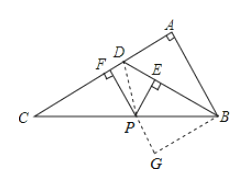
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 是
是![]() 上任一点,
上任一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() 是等腰三角形;②
是等腰三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论是( )
,其中正确的结论是( )

A.①②B.①③④C.①④D.①②③④
【答案】B
【解析】
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADB=∠C+∠DBC,然后求出∠C=∠DBC,再根据等角对等边可得DC=DB,从而判断①正确;没有条件说明∠C的度数,判断出②错误;连接PD,利用△BCD的面积列式求解即可得到PE+PF=AB,判断出③正确;过点B作BG∥AC交FP的延长线于G,根据两直线平行,内错角相等可得∠C=∠PBG,∠G=∠CFP=90°,然后求出四边形ABGF是矩形,根据矩形的对边相等可得AF=BG,根据然后利用“角角边”证明△BPE和△BPG全等,根据全等三角形对应边相等可得BG=BE,再利用勾股定理列式求解即可判断④正确.
在△BCD中,∠ADB=∠C+∠DBC,
∵∠ADB=2∠C,
∴∠C=∠DBC,
∴DC=DB,
∴△DBC是等腰三角形,故①正确;
无法说明∠C=30°,故②错误;
连接PD,则S△BCD=![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() DCAB,
DCAB,
∴PE+PF=AB,故③正确;
过点B作BG∥AC交FP的延长线于G,
则∠C=∠PBG,∠G=∠CFP=90°,
∴∠PBG=∠DBC,四边形ABGF是矩形,
∴AF=BG,
在△BPE和△BPG中,
 ,
,
∴△BPE≌△BPG(AAS),
∴BG=BE,
∴AF=BE,
在Rt△PBE中,PE2+BE2=BP2,
即PE2+AF2=BP2,故④正确.
综上所述,正确的结论有①③④.
故选:B.

【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.