题目内容
【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.

【答案】(1)作图见解析;(2)证明见解析.
【解析】试题分析:(1)作出线段AC的垂直平分线进而得出AC垂直平分线与线段AB的交点O,进而以AO为半径做圆即可.
(2)连接CO,由圆周角定理和三角形内角和定理,利用已知得出∠OCB=90°,进而求出即可.
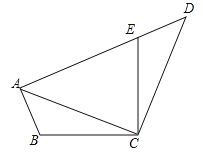
试题解析:解:(1)作图如答图1:

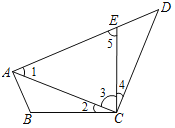
(2)证明:如答图2,连接OC,
∵OA=OC,∠A=25°,∴∠BOC=50°.
又∵∠B=40,∴∠BOC+∠B=90°.
∴∠OCB=90°.
∴OC⊥BC.
∴BC是⊙O的切线.


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目