题目内容
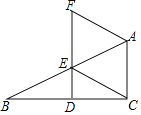
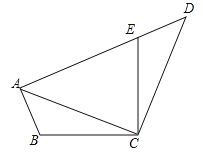
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析: ![]() 根据同角的余角相等可得到
根据同角的余角相等可得到![]() 结合条件
结合条件![]() ,再加上
,再加上![]() 可证得结论;
可证得结论;![]() 根据
根据![]() 得到
得到![]() 根据等腰三角形的性质得到
根据等腰三角形的性质得到![]() 由平角的定义得到
由平角的定义得到![]()
试题解析: ![]() 证明:
证明:
![]()
![]()
![]()
在△ABC和△DEC中,  ,
,
![]()
![]()
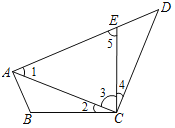
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?

【答案】面积等于36
【解析】试题分析:利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°,分别求![]() 的面积.
的面积.
试题解析:
![]() ∠B=90°,AB=3,BC=4,AC=
∠B=90°,AB=3,BC=4,AC=![]()
![]() =169,
=169,
所以∠ACD=90°,
![]() .
.
所以面积是36.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.