题目内容
(本题8分)
某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角.

(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变。
小题1:①求树与地面成45°角时的影长。
小题2:②试求树影的最大长度.
(计算结果精确到0.1米,参考数据: ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角.

(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变。
小题1:①求树与地面成45°角时的影长。
小题2:②试求树影的最大长度.
(计算结果精确到0.1米,参考数据:
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)小题1:(1)⒌1
小题2:(2)① ⒐6 ②⒑2
分析:
(1)在直角△ABC中,已知∠ACB=30°,AC=12米.利用三角函数即可求得AB的长;
(2)①在△AB1C1中,已知AB1的长,即AB的长,∠B1AC1=45°,∠B1C1A=30°.过B1作AC1的垂线,在直角△AB1N中根据三角函数求得AN,BN;再在直角△B1NC1中,根据三角函数求得NC1的长,即可求解;
②当树与地面成60°角时影长最大,根据三角函数即可求解。
解答:
(1)AB=ACtan30°=9×
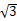 /3=3
/3=3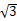 =5.1(米)
=5.1(米)答:树高约为5.1米。
(2)作B1N⊥AC1于N。
①如图(2):
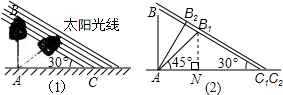
B1N=AN=AB1sin45°=3
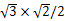 ≈3.5(米),
≈3.5(米),NC1=NB1tan60°=3
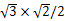 ×
×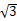 ≈6.1(米),
≈6.1(米),AC1=AN+NC1=3.5+6.1=9.6(米)。
答:树与地面成45°角时的影长约为9.6米。
②如图(2),当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2≈10.2米
答:树的最大影长约为10.2米。
点评:一般三角形的计算可以通过作高线转化为直角三角形的问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
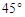 .为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为
.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为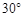 ,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?
,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?
 的值等于
的值等于


 的坡面向上走50米,则此人离地面的高度为( )
的坡面向上走50米,则此人离地面的高度为( )
 x=2sin45°-1
x=2sin45°-1 ,AC=18,求BC、AB的长.
,AC=18,求BC、AB的长.