题目内容
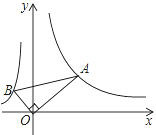
【题目】如图,在ABCD中,AB⊥BD,sinA=![]() ,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=
,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=![]() (k>0)同时经过B、D两点,则点B的坐标是_____.
(k>0)同时经过B、D两点,则点B的坐标是_____.

【答案】(![]() ,
,![]() ).
).
【解析】
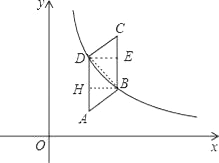
连结DB,作BH⊥AD于H,DE⊥BC于E,如图,
∵AB⊥BD,∴∠ABD=90°,
在Rt△ABD中,sin∠A=![]() =
=![]() ,
,
设BD=4t,则AD=5t,∴AB=![]() =3t,
=3t,
在Rt△ABH中,∵sin∠A=![]() ,
,
∴BH=![]() ×3t=
×3t= ![]() t,
t,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=5t,CD=AB=3t,
而AD⊥x轴,∴BC⊥x轴,
在Rt△CDE中,CE=![]() ,
,
∴D(1,k),点C的纵坐标为3,
∴B(1+![]() ,3﹣5t),k=3﹣
,3﹣5t),k=3﹣![]() ,
,
∵1k=(1+ ![]() )(3﹣5t),即3﹣
)(3﹣5t),即3﹣![]() =(1+
=(1+ ![]() )(3﹣5t),
)(3﹣5t),
整理得3t2﹣t=0,解得t1=0(舍去),t2=![]() ,
,
∴B ![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目