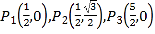��Ŀ����
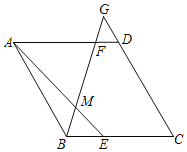
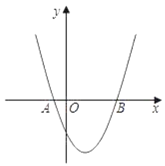
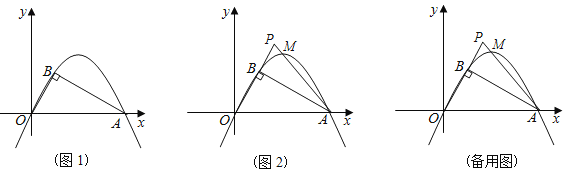
����Ŀ����ͼ1��������y��ax2+bx����ԭ��O�͵�A��12��0������B���������ϣ���֪OB��BA���ҡ�A��30�㣮
��1����������ߵĽ���ʽ��
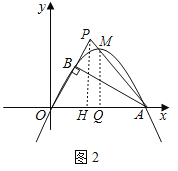
��2����ͼ2����PΪOB�ӳ�����һ�㣬������AP���������ڵ�M�����P�ĺ�����Ϊt����M�ĺ�����Ϊm�����ú���t�Ĵ���ʽ��ʾm����Ҫ��дȡֵ��Χ��
��3���ڣ�2���������£�����O��OW��AP��W�������߶�AB�ڵ�G������W��ֱ�߽�OP�ӳ����ڵ�N����x���ڵ�K������WKA��2��OAP����NK��11�����M�ĺ����꼰WG�ij���
���𰸡���1��y����![]() ����2��m��
����2��m��![]() ����3��M��ĺ�����Ϊ
����3��M��ĺ�����Ϊ![]() ��WG��
��WG��![]()
��������
��1�������B�����꣬��A��B������������������y��ax2+bx���ɵý⣻
��2������P��PH��OA�ڵ�H������M��MQ��OA�ڵ�Q��P(t��![]() t)��M(m����
t)��M(m����![]() )����PH��MQ�ɵ�
)����PH��MQ�ɵ�![]() ����ɵó��𰸣�
����ɵó��𰸣�
��3��ȡOA���е�R������WR��֤��WR��WK�����WN��11��6��5����֤����POW��2��N��ȡOP���е㣬����TW��֤�á�N����NTW�����OP��10�������t��m��ֵ�����tan![]() ����OW��12��
����OW��12��![]() �������OG�ij�����𰸿������
�������OG�ij�����𰸿������
�⣺��1������B��BD��OA�ڵ�D��
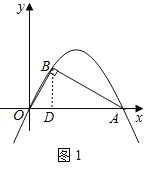
��A(12��0)��
��OA��12��
�ߡ�A��30����
��OB=6��
��AB=6![]() ��
��
��![]() ��
��
��B(3��3![]() )��
)��
��������y��ax2+bx������B(3��3![]() )�͵�A(12��0)��
)�͵�A(12��0)��
��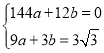 ��
��
���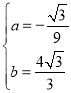 ��
��
��y����![]() ��
��
��2������P��PH��OA�ڵ�H������M��MQ��OA�ڵ�Q��P(t��![]() t)��M(m����
t)��M(m����![]() )��
)��
��PH//MQ��
���APH=��AMQ��
�ߡ�AHP=��AQM=90�㣬
���APH�ס�AMQ��
��![]() ��
��
��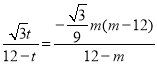 ��
��
��![]() ��
��
��![]() ��
��
��m��![]() ��
��
��3��ȡOA���е�R������WR��
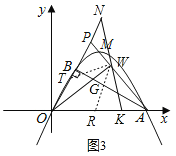
��OW��AP��
��WR��RA��OR��
���OAP����RWA��
���ORW��2��OAP��
�ߡ�WKA��2��OAP��
���ORW����WKA��
���WRK����WKO��
��WR��WK��
��![]() ��
��
��NW��NK��WK��11��6��5��
�ߡ�POW����BAW����OAP����OAB������30����
��N����AKW����AOB��2����60����
���POW��2��N��
ȡOP���е㣬����TW��
���N����NTW��
��![]() ��
��
��OP��10��
��t2+3t2��100��
��t��5��
��![]() ��
��![]() ��
��
��M��ĺ�����Ϊ![]() ��
��
����P��x��ľ�����5![]() ��
��
��tan![]() ��
��
��OW��AW��OA��5![]() ��7��2
��7��2![]() ��
��
��OW��12��![]() ��
��
����![]() ��
��![]() ��OA��12��
��OA��12��
��![]() ��
��![]() ��
��
��WG��![]() ��
��

����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ