题目内容
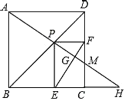
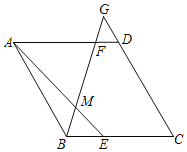
【题目】如图,在菱形ABCD中,E在BC上,G在CD延长线上,AE和BG相交于点M,若AE=BG,tan∠BME=2,菱形ABCD面积为![]() ,则AB的长_____.
,则AB的长_____.
【答案】![]()
【解析】
作BK⊥CD于K,作EN⊥AD于N,作DH⊥BC于H;根据全等三角形的性质得到∠EAN=∠G,设DH=2k,CH=k,由勾股定理得到CD=![]() k,于是得到结论.
k,于是得到结论.
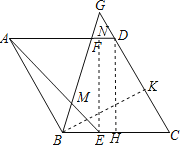
解:作BK⊥CD于K,作EN⊥AD于N,作DH⊥BC于H;如图所示:
∵四边形ABCD是菱形,
∴AD=CD,ADEN=CDBK,
∴BK=EN,
在Rt△AEN和Rt△BGK中,![]() ,
,
∴Rt△AEN≌Rt△BGK(HL),
∴∠EAN=∠G,
∵∠AFM=∠GFD,
∴∠BME=∠AFM=∠ADK=∠C,
∴tan∠C=tan∠BME=2,
设DH=2k,CH=k,
则CD=![]() k,
k,
根据题意得:菱形ABCD的面积=![]() k2k=
k2k=![]() ,
,
解得:k=![]() ,
,
∴AB=CD=![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
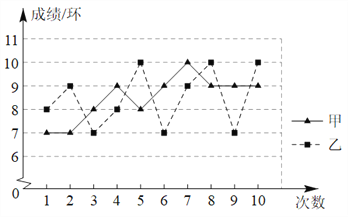
(1)根据折线图把下列表格补充完整;
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.