ћвƒњƒЏ»Ё
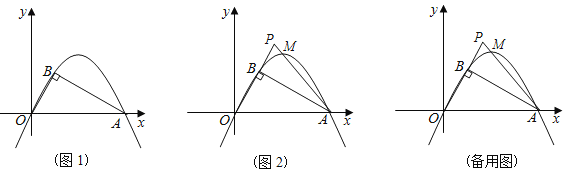
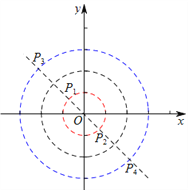
°Њћвƒњ°њ‘Џ∆љ√ж÷±љ«„ш±кѕµ![]() ÷–µƒµгPЇЌЌЉ–ќM£ђЄш≥ц»зѕ¬µƒґ®“е£Ї»ф‘ЏЌЉ–ќMіж‘Џ“їµгQ£ђ єµ√P°ҐQЅљµгЉдµƒЊајл–°”Џїтµ»”Џ1£ђ‘т≥∆Pќ™ЌЉ–ќMµƒєЎЅ™µг£Ѓ
÷–µƒµгPЇЌЌЉ–ќM£ђЄш≥ц»зѕ¬µƒґ®“е£Ї»ф‘ЏЌЉ–ќMіж‘Џ“їµгQ£ђ єµ√P°ҐQЅљµгЉдµƒЊајл–°”Џїтµ»”Џ1£ђ‘т≥∆Pќ™ЌЉ–ќMµƒєЎЅ™µг£Ѓ
£®1£©µ±°—Oµƒ∞лЊґќ™2 ±£ђ
Ґў‘Џµг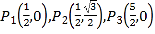 ÷–£ђ°—OµƒєЎЅ™µг «_______________£Ѓ
÷–£ђ°—OµƒєЎЅ™µг «_______________£Ѓ
ҐЏµгP‘Џ÷±ѕяy=-x…ѕ£ђ»фPќ™°—O µƒєЎЅ™µг£ђ«уµгPµƒЇб„ш±кµƒ»°÷µЈґќІ£Ѓ
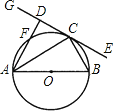
£®2£©°—C µƒ‘≤–ƒ‘Џx÷б…ѕ£ђ∞лЊґќ™2£ђ÷±ѕяy=-x+1”лx÷б°Ґy÷бљї”ЏµгA°ҐB£Ѓ»фѕяґќAB…ѕµƒЋщ”–µгґЉ «°—CµƒєЎЅ™µг£ђ÷±љ”–і≥ц‘≤–ƒCµƒЇб„ш±кµƒ»°÷µЈґќІ£Ѓ
°Њір∞Є°њ£®1£©ҐўP2°ҐP3£ђҐЏ£≠![]() °№x°№£≠
°№x°№£≠![]() їт
їт![]() °№x°№
°№x°№![]() £ї£®2£©£≠2°№x°№1їт2°№x°№2
£ї£®2£©£≠2°№x°№1їт2°№x°№2![]() .
.
°Њљвќц°њ
‘ћв£®1£©Ґў”…ћв“вµ√£ђP÷ї–и‘Џ“‘Oќ™‘≤–ƒ£ђ∞лЊґќ™1ЇЌ3Ѕљ‘≤÷ЃЉдЉіњ…£ђ”…![]() µƒ÷µњ…÷™
µƒ÷µњ…÷™![]() ќ™°—OµƒєЎЅ™µг£їҐЏ¬ъ„гћхЉюµƒP÷ї–и‘Џ“‘Oќ™‘≤–ƒ£ђ∞лЊґќ™1ЇЌ3Ѕљ‘≤÷ЃЉдЉіњ…£ђЋщ“‘PЇб„ш±кЈґќІ «£≠
ќ™°—OµƒєЎЅ™µг£їҐЏ¬ъ„гћхЉюµƒP÷ї–и‘Џ“‘Oќ™‘≤–ƒ£ђ∞лЊґќ™1ЇЌ3Ѕљ‘≤÷ЃЉдЉіњ…£ђЋщ“‘PЇб„ш±кЈґќІ «£≠![]() °№x°№£≠
°№x°№£≠![]() їт
їт![]() °№x°№
°№x°№![]() £ї
£ї
£®2£©.Ј÷Ћƒ÷÷«йњцћ÷¬џЉіњ…£ђµ±‘≤єэµгA£ђ CA=3 ±£їµ±‘≤”л–°‘≤ѕа«– ±£їµ±‘≤єэµг A£ђAC=1 ±£їµ±‘≤єэµг B ±£ђЉіњ…µ√≥ц.
‘ћвљвќц£Ї
£®1£©![]() £ђ
£ђ
µг![]() ”л°—µƒ„о–°Њајлќ™
”л°—µƒ„о–°Њајлќ™![]() £ђµг
£ђµг![]() ”л°—µƒ„о–°Њајлќ™1£ђµг
”л°—µƒ„о–°Њајлќ™1£ђµг![]() ”л°—µƒ„о–°Њајлќ™
”л°—µƒ„о–°Њајлќ™![]() £ђ
£ђ
°а°—µƒєЎЅ™µгќ™![]() ЇЌ
ЇЌ![]() £Ѓ
£Ѓ
ҐЏЄщЊЁґ®“еЈ÷ќц£ђњ…µ√µ±÷±ѕяy=-x…ѕµƒµгPµљ‘≠µгµƒЊајл‘Џ1µљ3÷ЃЉд ±ЈыЇѕћв“в£ї
°а …иµгPµƒ„ш±кќ™P (x £ђ-x) £ђ
µ±OP=1 ±£ђ”…ЊајлєЂ љњ…µ√£ђOP=![]() £ђљвµ√
£ђљвµ√![]() £ђµ±OP=3 ±£ђ”…ЊајлєЂ љњ…µ√£ђOP=
£ђµ±OP=3 ±£ђ”…ЊајлєЂ љњ…µ√£ђOP=![]() £ђ
£ђ![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ
°а µгµƒЇб„ш±кµƒ»°÷µЈґќІќ™£≠![]() °№x°№£≠
°№x°№£≠![]() їт
їт![]() °№x°№
°№x°№![]()
£®2£©°яy=-x+1”л÷б°Ґ÷бµƒљїµгЈ÷±рќ™A°ҐBЅљµг£ђ°а Ѕоy=0µ√£ђ-x+1=0£ђљвµ√x=1£ђ
Ѕоµ√x=0µ√£ђy=0£ђ
°аA(1£ђ0) £ђB (0£ђ1) £ђ
Ј÷ќцµ√£Ї
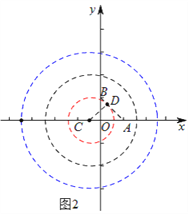
»зЌЉ1£ђµ±‘≤єэµгA ±£ђіЋ ±CA=3£ђ
°а µгC„ш±кќ™£ђC ( -2£ђ0)

»зЌЉ2£ђµ±‘≤”л–°‘≤ѕа«– ±£ђ«–µгќ™D£ђ
°аCD=1 £ђ
”÷°я÷±ѕяABЋщ‘ЏµƒЇѓ эљвќц љќ™y=-x+1£ђ
°а ÷±ѕяAB”лx÷б–ќ≥…µƒЉ–љ« «45°г£ђ
°а RT°чACD÷–£ђCA=![]() £ђ
£ђ
°а Cµг„ш±кќ™ (1-![]() £ђ0)
£ђ0)
°а CµгµƒЇб„ш±кµƒ»°÷µЈґќІќ™£ї-2°№![]() °№1-
°№1-![]() £ђ
£ђ
»зЌЉ3£ђµ±‘≤єэµгA ±£ђAC=1£ђ
Cµг„ш±кќ™(2£ђ0)

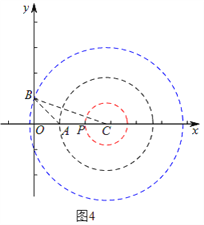
»зЌЉ4£ђ
µ±‘≤єэµг B ±£ђЅђљ” BC £ђіЋ ± BC =3£ђ
‘Џ Rt°чOCB÷–£ђ”…єіє…ґ®јнµ√OC=![]() £ђ Cµг„ш±кќ™ (2
£ђ Cµг„ш±кќ™ (2![]() £ђ0)£Ѓ
£ђ0)£Ѓ
°а CµгµƒЇб„ш±кµƒ»°÷µЈґќІќ™2°№![]() °№2
°№2![]() £ї
£ї
°а„џ…ѕЋщ цµгCµƒЇб„ш±кµƒ»°÷µЈґќІќ™£≠![]() °№
°№![]() °№£≠
°№£≠![]() їт
їт![]() °№
°№![]() °№
°№![]() £Ѓ
£Ѓ

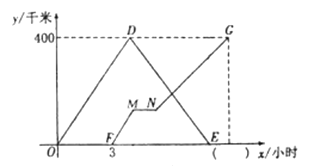
°Њћвƒњ°њ»зЌЉ «Љ„°Ґ““Ѕљ√ы…дїч‘Ћґѓ‘±µƒ10іќ…дїч≤в ‘≥…Љ®µƒ’џѕяЌ≥Љ∆ЌЉ.
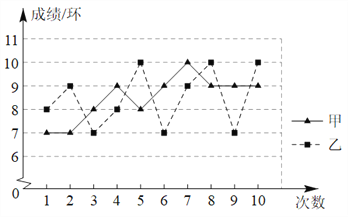
£®1£©ЄщЊЁ’џѕяЌЉ∞—ѕ¬Ѕ–±нЄс≤є≥дЌк’ы£ї
‘Ћґѓ‘± | ∆љЊщ э | ÷–ќї э | ÷Џ э |
Љ„ | 8.5 | 9 | |
““ | 8.5 |
£®2£©ЄщЊЁ…ѕ цЌЉ±н‘Ћ”√Ћщ—ІЌ≥Љ∆÷™ ґґ‘Љ„°Ґ““Ѕљ√ы‘Ћґѓ‘±µƒ…дїчЋЃ∆љљш––∆јЉџ≤ҐЋµ√чјн”….