题目内容
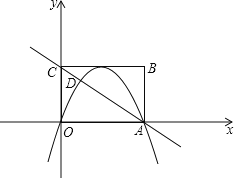
【题目】如图,直线y=4﹣x与双曲线y![]() 交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.

【答案】(﹣1,1)和(2,1).
【解析】
求得交点A、B的坐标,即可求得直径AB的长度和P点的坐标,从而求得PE的长度,利用勾股定理求得EM=EN=![]() ,结合P的坐标即可求得以OA为直径的圆与直线BC的交点坐标.
,结合P的坐标即可求得以OA为直径的圆与直线BC的交点坐标.
由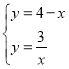 求得
求得![]() 或
或![]() ,
,
∴A(1,3),B(3,1),
∴OA![]() ,
,
设OA的中点为P,以AB为直径的⊙P与直线BC的交点为M、N,
过P点作PD⊥x轴于D,交BC于E,连接PN,
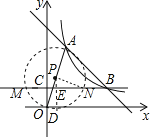
∵P是OA的中点,
∴P(![]() ,
,![]() ),
),
∴PD![]() ,
,
∵BC⊥y轴,垂足为C,
∴BC∥x轴,
∴PD⊥BC,
∴PE![]() 1
1![]() ,
,
在Rt△PEN中,EM=EN![]() ,
,
∴M(﹣1,1),N(2,1).
∴以OA为直径的圆与直线BC的交点坐标是(﹣1,1)和(2,1),
故答案为(﹣1,1)和(2,1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】綦江区某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手,每队中每个队员的身高(单位:cm)如下:
甲队 | 178 | 177 | 179 | 179 | 178 | 178 | 177 | 178 | 177 | 179 |
乙队:

分析数据:两组样本数据的平均数、中位数、众数、方差如下表所示:
整理、描述数据:
平均数 | 中位数 | 众数 | 方差 | |
甲队 | 178 | 178 | b | 0.6 |
乙队 | 178 | a | 178 | c |
(1)表中a=______,b=______,c=______;
(2)根据表格中的数据,你认为选择哪个队比较好?请说明理由.