题目内容
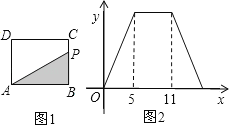
【题目】如图,正方形![]() 中,
中, ![]() ,点
,点![]() 在边
在边![]() 上,且,
上,且,![]() 将
将![]() 沿
沿![]() 翻折至
翻折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]()
(2)求证:![]() ;
;
(3)求![]() 的面积.
的面积.
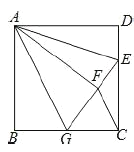
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)由轴对称可以得出AF=AD,∠D=∠AFE=90°,得出∠AFG=90°,根据正方形的性质可以得出AF=AB,根据HL就可以判断△ABG≌△AFG.
(2)由条件可以求出ED的值,设FG=x,则BG=FG=x,CG=6-x,EG=x+2,由勾股定理可以求出x的值,从而可以求出BG和CG的值,得出结论.
(3)过点F作FN⊥CG于点N,可以得出∠FNG=∠DCG=90°,通过证明△GFN∽△GEC,得出![]() ,可以求出FN的值,最后利用三角形的面积公式可以求出其面积.
,可以求出FN的值,最后利用三角形的面积公式可以求出其面积.
(1)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵将![]() 对折得到
对折得到![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
(2)证明: ∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
, ![]() ,
,![]() ,
,
在直角三角形![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,
,
解得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
(3)过点![]() 作
作![]() 于点
于点![]() ,
,
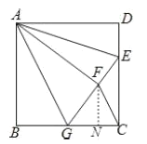
则![]() ,
,
又∵∠FGN=∠EGC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴FN=![]() ,
,
∴S△CGF=![]() CGFN=
CGFN=![]() ×
×![]() ×3=
×3=![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目