题目内容
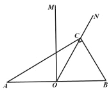
【题目】在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连结CD,将CD绕C点逆时针旋转90°至CE,连结DE,过C作CF⊥DE交AB于F,连结BE.
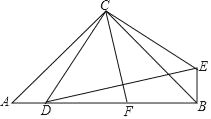
(1)求证:AD=BE;
(2)求证:AD2+BF2=DF2;
(3)若∠ACD=15°,CD=![]() +1,求BF.
+1,求BF.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)将CD绕C点逆时针旋转90°至CE,可得△DCE是等腰直角三角形,再判定△ACD≌△BCE(SAS),即可得出AD=BE;
(2)连接FE,根据CF是DE的垂直平分线,可得DF=EF,再根据Rt△BEF中,BE2+BF2=EF2,即可得出AD2+BF2=DF2;
(3)根据∠BDE=15°=∠DEF,可得∠BFE=30°,设BE=x,则BF=![]() x,EF=2x=DF,再根据Rt△BDE中,x2+(2x+
x,EF=2x=DF,再根据Rt△BDE中,x2+(2x+![]() x)2=(
x)2=(![]() +
+![]() )2,即可解得x=1,进而得到BF=
)2,即可解得x=1,进而得到BF=![]() .
.
(1)将CD绕C点逆时针旋转90°至CE,可得△DCE是等腰直角三角形,
∴∠DCE=∠ACB=90°,DC=EC,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
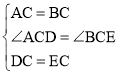 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
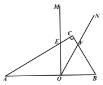
(2)如图,连接FE,
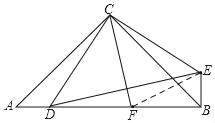
∵CF⊥DE,△DCE是等腰直角三角形,
∴CF是DE的垂直平分线,
∴DF=EF,
又∵△ACD≌△BCE,∠ABC=45°,
∴∠CBE=∠A=45°=∠ABC,
∴∠EBF=90°,
∴Rt△BEF中,BE2+BF2=EF2,
∴AD2+BF2=DF2;
(3)∵CD=![]() +1,△DCE是等腰直角三角形,
+1,△DCE是等腰直角三角形,
∴DE=![]() ,
,
∵∠ACD=15°,∠A=∠CDE=45°,
∴∠BDE=15°=∠DEF,
∴∠BFE=30°,
设BE=x,则BF=![]() x,EF=2x=DF,
x,EF=2x=DF,
∴Rt△BDE中,x2+(2x+![]() x)2=(
x)2=(![]() +
+![]() )2,
)2,
解得x=1,
∴BF=![]() .
.

【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 |
|
|
|
|
| ······ |
油箱中的剩余油量 |
|
|
|
|
| ····· |
(1)在这个问题中,自变量是_ 因变量是_ ;
(2)该轿车油箱的容量为__ L,行驶![]() 时,估计油箱中的剩余油量为____
时,估计油箱中的剩余油量为____![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请估计
,请估计![]() 两地之间的距离.
两地之间的距离.