题目内容
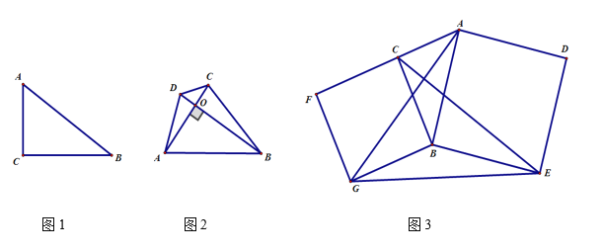
【题目】在直角三角形中,两直角边的平方和等于斜边的平方.如图1,若在△ABC中,∠C=90°,则AC2+BC2=AB2.我们定义为“商高定理”.
(1)如图1,在△ABC中,∠C=90°中,BC=4,AB=5,试求AC=__________;
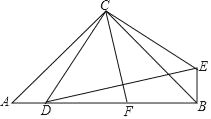
(2)如图2,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;
(3)如图3,分别以Rt△ACB的直角边BC和斜边AB为边向外作正方形BCFG和正方形ABED,连结CE、AG、GE.已知BC=4,AB=5,求GE2的值.
【答案】(1)AC=3; (2)见解析;(3)73.
【解析】
(1)根据勾股定理求出AC即可;
(2)在Rt△DOA中根据勾股定理有OD2+OA2=AD2,同理有OD2+OC2=CD2,OB2+OC2=BC2,OA2+OB2=AB2,又AB2+ CD2=OA2+OB2+ OD2+OC2,AD2+ BC2=OD2+OA2+ OB2+OC2
即可证明AB2+ CD2=AD2+ BC2;
(3)连接CG、AE,根据∠GBC=∠EBA=900得∠ABG=∠EBC,则证明△ABG≌△EBC,则∠1=∠2 ,∠3=∠4,由(2)可知AC2+GE2=CG2+AE2,则可求出CG2、AE2 、AC2从而求出GE2.
解:(1)在△ABC中,∠C=90°中,BC=4,AB=5
∴AC=![]() =3
=3
(2)在Rt△DOA中,∠DOA=900,
∴OD2+OA2=AD2
同理:OD2+OC2=CD2
OB2+OC2=BC2
OA2+OB2=AB2
∵AB2+ CD2=OA2+OB2+ OD2+OC2
AD2+ BC2=OD2+OA2+ OB2+OC2
∴AB2+ CD2=AD2+ BC2
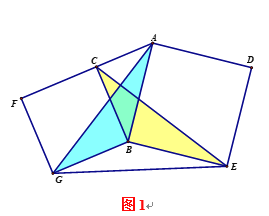
(3)∵∠GBC=∠EBA=900
∴∠GBC+∠CBA=∠EBA+∠CBA
∴∠ABG=∠EBC
如图1,在△ABG和△EBC中
∴△ABG≌△EBC(SAS)
∴如图2,∠1=∠2 ,∠3=∠4
∴∠5=∠AIJ=900
∴AG⊥CB
连接CG、AE,
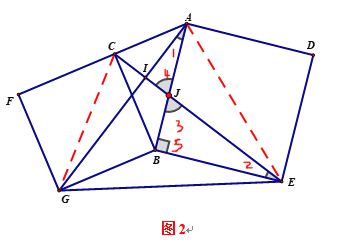
由(2)可知
AC2+GE2=CG2+AE2
在Rt△CBG中,CG2=BC2+BG2
CG2=42+42=32
在Rt△ABE中,AE2=BE2+AB2
AE2=52+52=50
在Rt△ABC中,AB2=AC2+BC2
52=AC2+42
AC2=9
∴AC2+GE2=CG2+AE2
9+ GE2=32+50
GE2=73