题目内容
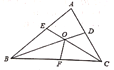
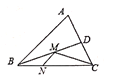
【题目】如图，在锐角三角形ABC中，AB=4，△ABC的面积为8，BD平分∠ABC。若M、N分别是BD、BC上的动点，则CM+MN的最小值是（ ）
A. 2 B. 4 C. 6 D. 8
【答案】B
【解析】
过点C作CE⊥AB于点E，交BD于点M′，过点M′作M′N′⊥BC于N′，则CE即为CM+MN的最小值，再根据三角形的面积公式求出CE的长，即为CM+MN的最小值．
解：过点C作CE⊥AB于点E，交BD于点M′，过点M作MN′⊥BC于N′，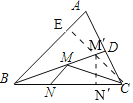
∵BD平分∠ABC，M′E⊥AB于点E，M′N′⊥BC于N
∴M′N′=M′E，
∴CE=CM′+M′E
∴当点M与M′重合，点N与N′重合时，CM+MN的最小值．
∵三角形ABC的面积为8，AB=4，
∴
×4CE=8，
∴CE=4．
即CM+MN的最小值为4．
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
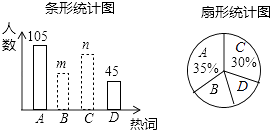
【题目】2018年6月上海语文把小学教材中“外婆”改成“姥姥一事，引起社会的广泛关注和讨论，明德集团某校文学社就此召开了一次研讨会，为了传承中国传统文化，并组织了一次全体学生“汉字听写”大赛，每位学生听写汉字39个，随机抽取了部分学生的听写结果作为样本进行整理，绘制成如下的统计图表：
组别 | 正确字数x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根据以上信息完成下列问题：
(1)统计表中的m＝ ，n＝ ，并补全条形统计图；
(2)扇形统计图中“C组“所对应的圆心角的度数是 ；
(3)已知该校共有600名学生，如果听写正确的字的个数不少于24个定为合格，请你估计该校本次听写比赛合格的学生人数．
