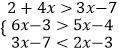Question

【题目】阅读下列文字与例题，并解答。

将一个多项式分组进行因式分解后，可用提公因式法或公式法继续分解的方法称作分组分解法。例如：以下式子的分解因式的方法叉称为分组分解法。

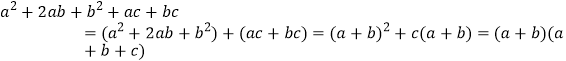（1）试用“分组分解法”分解因式：

（2）已知四个实数a,b,c,d满足。并且，，，同时成立。

①当k=1时，求a+c的值；

②当k≠0时，用含a的代数式分别表示b、c、d。

Answer 1

【答案】（1）（x﹣y）（x+y+z）；（2）①a+c=±6；②c=2a，b=d=﹣3a．

【解析】

（1）根据因式分解-分组分解法分解即可；
（2）根据因式分解-分组分解法和提公因式法分解即可．

解：（1）x2﹣y2+xz﹣yz=（x+y）（x﹣y）+z（x﹣y）

=（x﹣y）（x+y+z）；

（2）①当k=1 时，得a2+ac=12，c2+ac=24，

（a2+ac）+（c2+ac）=a（a+c）+c（a+c）=（a+c）（a+c）=（a+c）2=12+24=36，

∴a+c=±6；

②∵当k≠0时，由a2+ac=12k，b2+bc=12k，得（a2+ac）﹣（b2+bc）=0，

即a2﹣b2+ac﹣bc=0，∴（a﹣b）（a+b+c）=0，

∵a≠b，∴a+b+c=0，∴b=﹣a﹣c．

由c2+ac=24k，d2+ad=24k，得（c2+ac）﹣（d2+ad）=0，即c2﹣d2+ac﹣ad=0，

∴（c﹣d）（c+d+a）=0，∵c≠d，∴c+d+a=0，∴d=﹣a﹣c，

∴b=d=﹣a﹣c，

又∵（a2+ac）×2=c2+ac=24k，∴2a（a+c）﹣c（c+a）=0，

即（a+c）（2a﹣c）=0，∴a+c=0或2a﹣c=0，

∴c=﹣a，或c=2a，又k≠0，则c=2a，

∴c=2a，b=d=﹣3a．