Question

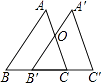
【题目】如图，△ABC中，AB=AC，E在BA的延长线上，AD平分∠CAE．
（1）求证：AD∥BC；
（2）过点C作CG⊥AD于点F，交AE于点G，若AF=4，求BC的长．

Answer 1

【答案】
（1）证明：∵AD平分∠CAE，

∴∠DAG= ∠CAG，

∵AB=AC，

∴∠B=∠ACB，

∵∠CAG=∠B+∠ACB，

∴∠B= ∠CAG，

∴∠B=∠DAG，

∴AD∥BC

（2）解：∵CG⊥AD，

∴∠AFC=∠AFG=90°，

在△AFC和△AFG中，

，

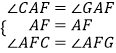∴△AFC≌△AFG（ASA），

∴CF=GF，

∵AD∥BC，

∴△AGF∽△BGC，

∴GF：GC=AF：BC=1：2，

∴BC=2AF=2×4=8

【解析】（1）由AB=AC，AD平分∠CAE，易证得∠B=∠DAG= ∠CAG，继而证得结论；（2）由CG⊥AD，AD平分∠CAE，易得CF=GF，然后由AD∥BC，证得△AGF∽△BGC，再由相似三角形的对应边成比例，求得答案．