题目内容
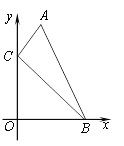
【题目】如图,在平面直角坐标系xOy中,已知![]() ,
,![]() ,矩形OABC的对角线交于点P,点M在经过点P的函数
,矩形OABC的对角线交于点P,点M在经过点P的函数![]() 的图象上运动,k的值为__________,OM长的最小值__________.
的图象上运动,k的值为__________,OM长的最小值__________.

【答案】12 ![]()
【解析】
先求出P(4,3),求得k=4×3=12,进而得出y=![]() ,再根据双曲线的对称性可得,当点M在第一象限角平分线上时,OM最短,即当x=y时,x=
,再根据双曲线的对称性可得,当点M在第一象限角平分线上时,OM最短,即当x=y时,x=![]() ,解得x值,进而求出点M的坐标,从而得到OM的最小值.
,解得x值,进而求出点M的坐标,从而得到OM的最小值.
解:∵A(8,0),C(0,6),矩形OABC的对角线交于点P,
∴P(4,3),
代入函数![]() 可得,k=4×3=12,
可得,k=4×3=12,
∴y=![]() ,
,
∵点M在经过点P的函数y=![]() (x>0)的图象上运动,
(x>0)的图象上运动,
∴根据双曲线的对称性可得,当点M在第一象限角平分线上时,OM最短,
当x=y时,x=![]() ,
,
解得x=±![]() ,
,
又∵x>0,
∴x=![]() ,
,
∴M(![]() ,
,![]() ),
),
∴OM2=![]() =24,
=24,
∴OM=![]() .
.
故答案为:12;![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目