题目内容
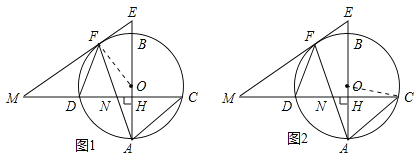
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OF,根据切线的性质结合四边形内角和为360°,即可得出∠M+∠FOH=180°,由三角形外角结合平行线的性质即可得出∠M=∠C=2∠OAF,再通过互余利用角的计算即可得出∠CAN=90°﹣∠OAF=∠ANC,由此即可证出CA=CN;
(2)连接OC,由圆周角定理结合cos∠DFA=![]() ,AN=
,AN=![]() ,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
试题解析:(1)证明:连接OF,则∠OAF=∠OFA,如图所示.
∵ME与⊙O相切,∴OF⊥ME.∵CD⊥AB,∴∠M+∠FOH=180°.
∵∠BOF=∠OAF+∠OFA=2∠OAF,∠FOH+∠BOF=180°,∴∠M=2∠OAF.
∵ME∥AC,∴∠M=∠C=2∠OAF.
∵CD⊥AB,∴∠ANC+∠OAF=∠BAC+∠C=90°,∴∠ANC=90°﹣∠OAF,∠BAC=90°﹣∠C=90°﹣2∠OAF,∴∠CAN=∠OAF+∠BAC=90°﹣∠OAF=∠ANC,∴CA=CN.
(2)连接OC,如图2所示.
∵cos∠DFA=![]() ,∠DFA=∠ACH,∴
,∠DFA=∠ACH,∴![]() =
=![]() .设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=
.设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=![]() =
=![]() =
=![]() a=
a=![]() ,∴a=2,AH=3a=6,CH=4a=8.
,∴a=2,AH=3a=6,CH=4a=8.
设圆的半径为r,则OH=r﹣6,在Rt△OCH中,OC=r,CH=8,OH=r﹣6,∴OC2=CH2+OH2,r2=82+(r﹣6)2,解得:r=![]() ,∴圆O的直径的长度为2r=
,∴圆O的直径的长度为2r=![]() .
.

 字词句段篇系列答案
字词句段篇系列答案