Question

【题目】在矩形ABCD中，AB＝1，BC＝2，点P是边BC上一点（点P不与点B，点C重合），点C关于直线AP的对称点为C'．

（1）如果C'落在线段AB的延长线上．

①在图①中补全图形；

②求线段BP的长度；

（2）如图②，设直线AP与CC'的交点为M，求证：BM⊥DM．

Answer 1

【答案】（1）①见解析;②PB＝;（2）见解析.

【解析】

（1）①根据要求画出图形即可；

②连接AC，作PH⊥AC于H．则△APB≌△APH，同侧AB＝AH＝1，PB＝PH，设PB＝PH＝x，利用勾股定理构建方程即可；

（2）如图②中，连接AC、BD交于点O．连接OM．只要证明A、B、M、C、D五点共圆，即可解决问题；

解：（1）①如图①所示：

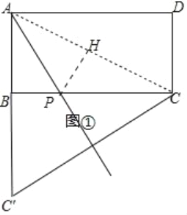
②连接AC，作PH⊥AC于H．则△APB≌△APH，

∴AB＝AH＝1，PB＝PH，设PB＝PH＝x，

∵AC＝＝，

∴CH＝﹣1，

在Rt△PCH中，x2+（﹣1）2＝（2﹣x）2，

解得x＝，

∴PB＝．

（2）如图②中，连接AC、BD交于点O．连接OM．

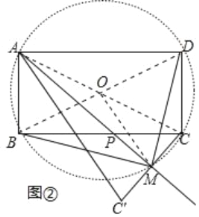
∵四边形ABCD是矩形，

∴OA＝OB＝OC＝OD，

∵∠AMC＝90°，

∴OM＝OA＝OB＝OC＝OD，

∴A、B、M、C、D五点共圆，

∵BD是直径，

∴∠BMD＝90°，

∴BM⊥DM．