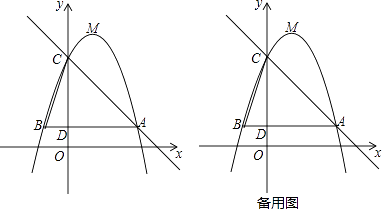
题目内容
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E. 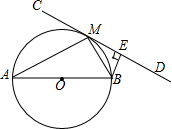
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE= ![]() ,sin∠BAM=
,sin∠BAM= ![]() ,求线段AM的长.
,求线段AM的长.
【答案】
(1)证明:如图,连接OM,
∵直线CD切⊙O于点M,
∴∠OMD=90°,
∴∠BME+∠OMB=90°,
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°,
∴∠BME=∠AMO,
∵OA=OM,
∴∠MAB=∠AMO,
∴∠BME=∠MAB

(2)证明:由(1)有,∠BME=∠MAB,
∵BE⊥CD,
∴∠BEM=∠AMB=90°,
∴△BME∽△BAM,
∴ ![]() ,
,
∴BM2=BEAB
(3)解:由(1)有,∠BME=∠MAB,
∵sin∠BAM= ![]() ,
,
∴sin∠BME= ![]() ,
,
在Rt△BEM中,BE= ![]() ,
,
∴sin∠BME= ![]() =
= ![]() ,
,
∴BM=6,
在Rt△ABM中,sin∠BAM= ![]() ,
,
∴sin∠BAM= ![]() =
= ![]() ,
,
∴AB= ![]() BM=10,
BM=10,
根据勾股定理得,AM=8
【解析】(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;(2)由(1)得出的结论和直角,判断出△BME∽△BAM,即可得出结论,(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.

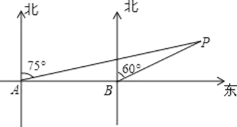
【题目】如图,某轮船由西向东航行,在 A 处测得小岛 P 的方位是北偏东 75°,又继续航行 8 海里后,在 B 处测得小岛 P 的方位是北偏东 60°,则此时△ABP 的面积为______平方海里.
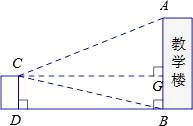
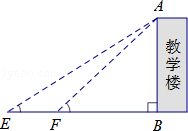
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)