题目内容
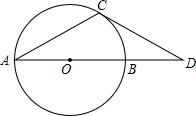
在Rt△ABC中,∠C=90°,AC=6,BC=8,点O在CB上,且AO平分∠BAC,CO=3(如图所示),以点O为圆心,r为半径画圆.
(1)r取何值时,⊙O与AB相切;
(2)r取何值时,⊙O与AB有两个公共点;
(3)当⊙O与AB相切时,设切点为D,在BC上是否存在点P,使△APD的面积为△ABC的面积的 一半?若存在,求出CP的长;若不存在,请说明理由.
一半?若存在,求出CP的长;若不存在,请说明理由.
(1)r取何值时,⊙O与AB相切;
(2)r取何值时,⊙O与AB有两个公共点;
(3)当⊙O与AB相切时,设切点为D,在BC上是否存在点P,使△APD的面积为△ABC的面积的
 一半?若存在,求出CP的长;若不存在,请说明理由.
一半?若存在,求出CP的长;若不存在,请说明理由.(1)过点D作DO⊥AB于D,
∵∠1=∠2,∠C=90°,
∴OD=OC=3,
故当r=3时,⊙O与AB相切;
(2)在Rt△AOC中,AO=
=
=3
,
而OB=BC-OC=8-3=5,
∴OA>OB
∴当3<r≤5时,⊙O与AB有两个公共点;
(3)连接OD,过点P做PH⊥AB于H;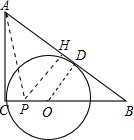
设CP=x,则PB=8-x,
∵D为切点,
∴OD⊥AB,
∴PH∥OD,
∴
=
,
=
,
∴PH=
(8-x),
∵AC⊥OC,
∴AC切⊙O于C,
∴AD=AC=6;
∴S△APD=
AD•PH=
×6×
(8-x)=
-
x;
由题意:S△APD=
S△ABC
∴
-
x=
×
×6×8
∴x=
;
故当PC=
时,存在P点,使S△APD=
S△ABC.
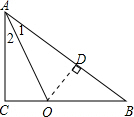
∵∠1=∠2,∠C=90°,
∴OD=OC=3,
故当r=3时,⊙O与AB相切;
(2)在Rt△AOC中,AO=
| AC2+OC2 |
| 62+32 |
| 5 |
而OB=BC-OC=8-3=5,
∴OA>OB
∴当3<r≤5时,⊙O与AB有两个公共点;
(3)连接OD,过点P做PH⊥AB于H;

设CP=x,则PB=8-x,
∵D为切点,
∴OD⊥AB,
∴PH∥OD,
∴
| PH |
| OD |
| PB |
| OB |
| PH |
| 3 |
| 8-x |
| 5 |
∴PH=
| 3 |
| 5 |
∵AC⊥OC,
∴AC切⊙O于C,
∴AD=AC=6;
∴S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 72 |
| 5 |
| 9 |
| 5 |
由题意:S△APD=
| 1 |
| 2 |
∴
| 72 |
| 5 |
| 9 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 4 |
| 3 |
故当PC=
| 4 |
| 3 |
| 1 |
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目