题目内容
【题目】如图,在Rt△ABC中,AB=AC=4![]() .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
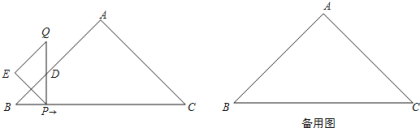
(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.
【答案】(1)当0<t≤4时,S=![]() t2,当4<t≤
t2,当4<t≤![]() 时,S=-
时,S=-![]() t2+8t-16,当
t2+8t-16,当![]() <t<8时,S=
<t<8时,S=![]() t2-12t+48;(2)
t2-12t+48;(2)![]() 秒或t2=(12-4
秒或t2=(12-4![]() )秒;(3)8.
)秒;(3)8.
【解析】
试题(1)当PQ过A时求出t=4,当E在AB上时求出t=![]() ,当P到C点时t=8,即分为三种情况:根据三角形面积公式求出当0<t≤4时,S=
,当P到C点时t=8,即分为三种情况:根据三角形面积公式求出当0<t≤4时,S=![]() t2,当4<t≤
t2,当4<t≤![]() 时,S=-
时,S=-![]() t2+8t-16,当
t2+8t-16,当![]() <t<8时,S=
<t<8时,S=![]() t2-12t+48;
t2-12t+48;
(2)存在,当点D在线段AB上时,求出QD=PD=t,PD=2t,过点A作AH⊥BC于点H,PH=BH-BP=4-t,在Rt△APH中求出AP=![]() ,
,
(ⅰ)若AP=PQ,则有![]() ,
,
(ⅱ)若AQ=PQ,过点Q作QG⊥AP于点G,根据△PGQ∽△AHP求出PG=![]() ,若AQ=PQ,得出
,若AQ=PQ,得出![]() .
.
(ⅲ)若AP=AQ,过点A作AT⊥PQ于点T,得出4=![]() ×2t,求出方程的解即可;
×2t,求出方程的解即可;
(3)四边形PMAN的面积不发生变化,连接AP,此时t=4秒,求出S四边形PMAN=S△APM+S△APN=S△CPN+S△APN=S△ACP=![]() ×CP×AP=8.
×CP×AP=8.
试题解析:(1)当0<t≤4时,S=![]() t2,当4<t≤
t2,当4<t≤![]() 时,S=-
时,S=-![]() t2+8t-16,当
t2+8t-16,当![]() <t<8时,S=
<t<8时,S=![]() t2-12t+48;(2)存在,理由如下:
t2-12t+48;(2)存在,理由如下:
当点D在线段AB上时,
∵AB=AC,
∴∠B=∠C=![]() (180°-∠BAC)=45°.
(180°-∠BAC)=45°.
∵PD⊥BC,
∴∠BPD=90°,
∴∠BDP=45°,
∴PD=BP=t,
∴QD=PD=t,
∴PQ=QD+PD=2t.
过点A作AH⊥BC于点H,
∵AB=AC,
∴BH=CH=![]() BC=4,AH=BH=4,
BC=4,AH=BH=4,
∴PH=BH-BP=4-t,
在Rt△APH中,AP=![]() ;
;
(ⅰ)若AP=PQ,则有![]() .
.
解得:![]() ,
,![]() (不合题意,舍去);
(不合题意,舍去);
(ⅱ)若AQ=PQ,过点Q作QG⊥AP于点G,如图(1),
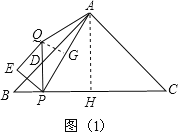
∵∠BPQ=∠BHA=90°,
∴PQ∥AH.
∴∠APQ=∠PAH.
∵QG⊥AP,
∴∠PGQ=90°,
∴∠PGQ=∠AHP=90°,
∴△PGQ∽△AHP,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
若AQ=PQ,由于QG⊥AP,则有AG=PG,即PG=![]() AP,
AP,
即![]() .
.
解得:t1=12-4![]() ,t2=12+4
,t2=12+4![]() (不合题意,舍去);
(不合题意,舍去);
(ⅲ)若AP=AQ,过点A作AT⊥PQ于点T,如图(2),
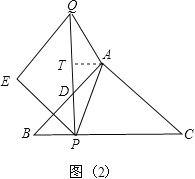
易知四边形AHPT是矩形,故PT=AH=4.
若AP=AQ,由于AT⊥PQ,则有QT=PT,即PT=![]() PQ,
PQ,
即4=![]() ×2t.解得t=4.
×2t.解得t=4.
当t=4时,A、P、Q三点共线,△APQ不存在,故t=4舍去.
综上所述,存在这样的t,使得△APQ成为等腰三角形,即![]() 秒或t2=(12-4
秒或t2=(12-4![]() )秒;
)秒;
(3)四边形PMAN的面积不发生变化.理由如下:
∵等腰直角三角形PQE,
∴∠EPQ=45°,
∵等腰直角三角形PQF,
∴∠FPQ=45°.
∴∠EPF=∠EPQ+∠FPQ=45°+45°=90°,
连接AP,如图(3),
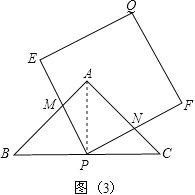
∵此时t=4秒,
∴BP=4×1=4=![]() BC,
BC,
∴点P为BC的中点.
∵△ABC是等腰直角三角形,
∴AP⊥BC,AP=![]() BC=CP=BP=4,∠BAP=∠CAP=
BC=CP=BP=4,∠BAP=∠CAP=![]() ∠BAC=45°,
∠BAC=45°,
∴∠APC=90°,∠C=45°,
∴∠C=∠BAP=45°,
∵∠APC=∠CPN+∠APN=90°,
∠EPF=∠APM+∠APN=90°,
∴∠CPN=∠APM,
∴△CPN≌△APM,
∴S△CPN=S△APM,
∴S四边形PMAN=S△APM+S△APN=S△CPN+S△APN=S△ACP=![]() ×CP×AP=
×CP×AP=![]() ×4×4=8.
×4×4=8.
∴四边形PMAN的面积不发生变化,此定值为8.
考点: 相似形综合题.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某学校20名数学教师的年龄(单位:岁)情况如下:29,42,58,37,53,52,49,24,37,46,42,55,40,38,50,26,54,26,44,52.
(1)填写下面的频率分布表:
分组 | 频数 | 频率 |
19.5~29.5 | ||
29.5~39.5 | ||
39.5~49.5 | ||
49.5~59.5 | ||
合计 |
(2)画出数据的频数分布直方图.