题目内容
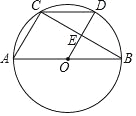
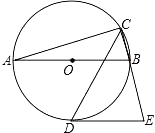
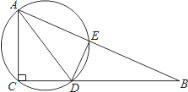
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)求BE的长;(2)求△ACD外接圆的半径.
【答案】(1)8;(2)![]() .
.
【解析】
(1)根据∠ACB=90°得到AD为圆O的直径,再根据直径所对的圆周角为直角可得三角形ADE为直角三角形,又AD是△ABC的角平分线,可得∠CAD=∠EAD,从而得到CD=ED,利用HL证明Rt△ACD与Rt△AED全等,得出AC=AE,再用AB-AE可求出EB的长
(2)由(1)∠AED=90°,得到DE与AB垂直,可得三角形BDE为直角三角形,设DE=CD=x,则BD=12-x,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CD的长,在直角三角形ACD中,由AC及CD的长,利用勾股定理即可求出AD的长,进而得出外接圆半径.
解:(1)∵∠ACB=90°,且∠ACB为圆O的圆周角(已知),
∴AD为圆O的直径(90°的圆周角所对的弦为圆的直径),
∴∠AED=90°(直径所对的圆周角为直角),
又AD是△ABC的角平分线(已知),
∴∠CAD=∠EAD(角平分线定义),
∴CD=DE(在同圆或等圆中,相等的圆周角所对的弦相等),
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE(全等三角形的对应边相等);
∵△ABC为直角三角形,且AC=5,CB=12,
∴根据勾股定理得:AB=![]() =13,
=13,
∴BE=13﹣AC=13﹣5=8;
(2)由(1)得到∠AED=90°,则有∠BED=90°,
设CD=DE=x,则DB=BC﹣CD=12﹣x,EB=AB﹣AE=AB﹣AC=13﹣5=8,
在Rt△BED中,根据勾股定理得:BD2=BE2+ED2 ,
即(12﹣x)2=x2+82 ,
解得:x=![]() ,
,
∴CD=![]() ,又AC=5,△ACD为直角三角形,
,又AC=5,△ACD为直角三角形,
∴根据勾股定理得:AD=![]() ,
,
根据AD是△ACD外接圆直径,
∴△ACD外接圆的半径为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某学校20名数学教师的年龄(单位:岁)情况如下:29,42,58,37,53,52,49,24,37,46,42,55,40,38,50,26,54,26,44,52.
(1)填写下面的频率分布表:
分组 | 频数 | 频率 |
19.5~29.5 | ||
29.5~39.5 | ||
39.5~49.5 | ||
49.5~59.5 | ||
合计 |
(2)画出数据的频数分布直方图.