��Ŀ����
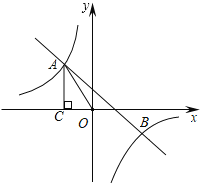
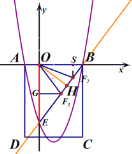
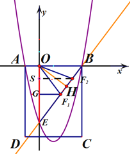
����Ŀ����ͼ�پ���ABCD������ϵ�е�λ����ͼ��ʾ��OB��3OA��3��BC��5�����߶�BC�Ƶ�B��ת��ʹ��C����y�Ḻ�����ϵĵ�E����������y��ax2+bx+c��a��0������A��B��C���㣮
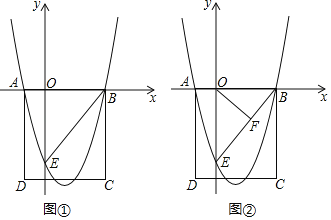
��1����������y��ax2+bx+c��a��0���Ľ���ʽ��
��2����P����������һ���㣬F��ֱ��BE��һ���㣮
����ͼ�ڣ���OF��BE��ֱ��PQ��OF��ֱ��BE�ڵ�Q������P��Q��F��OΪ������ı�����ƽ���ı��Σ����P�ĺ����ꣻ
����ֱ��OF��ֱ��BE�ļнǵ��ڡ�BEO��2������ֱ��д����F�����꣮
���𰸡���1��![]() ����2���ٷ��������ĵ�P�ĺ�������
����2���ٷ��������ĵ�P�ĺ�������![]() ��
��![]() ���ڷ��������ĵ�F��������(
���ڷ��������ĵ�F��������(![]() ,-2)����
,-2)����![]() ��
��![]() ��.
��.
��������
(1)�����OE�ij���Ȼ��ɵõ�A��B��E�����꣬����ɵ������ߵĽ���ʽ��
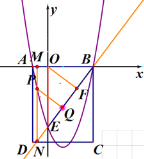
(2)����ͼ������P��ֱ��MN��![]() ���ڵ�M.��ֱ��BE�ڵ�N,�����BE�Ľ���ʽ��Ȼ���������PNQ�ա�OFE,�ֱ�������P��x����Ϸ��͵�P��x����·��ĺ�����ֵ���ɽ��
���ڵ�M.��ֱ��BE�ڵ�N,�����BE�Ľ���ʽ��Ȼ���������PNQ�ա�OFE,�ֱ�������P��x����Ϸ��͵�P��x����·��ĺ�����ֵ���ɽ��
����ͼ����OE�Ĵ�ֱƽ���߽�BE�ڵ�![]() ,��OH��BE�ڵ㣬����BE����
,��OH��BE�ڵ㣬����BE����![]() ���ڵ�H�ĶԳƵ�
���ڵ�H�ĶԳƵ�![]() �����
�����![]() �������
�������![]() �����ꣻ��
�����ꣻ��![]() ���ڵ�S,ͨ����ֱ��������
���ڵ�S,ͨ����ֱ��������![]() ,�������
,�������![]() �����꼴�ɽ��.
�����꼴�ɽ��.
(1) ������֪��OA=1,OB=3,BC=BE=5,
�ߡ�BOE=90,��OE=![]() ,
,
��A(-1,0),B(3,0),E(0,-4),
��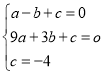 ����֮��
����֮��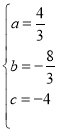 ��
��
�������ߵĽ���ʽΪ![]() ��
��
��2���ٹ���P��ֱ��MN��![]() ���ڵ�M.��ֱ��BE�ڵ�N,
���ڵ�M.��ֱ��BE�ڵ�N,
��ֱ��BE������B(3,0),E(0,-4)��
�ô���ϵ��������ֱ��BE�Ľ���ʽΪ![]()
��PQ��OF,OF��BE,��PQ��BE,
���ı���PQFOΪƽ���ı��Σ���PQ=FO=![]()
��MN��OE,���OEF=��PNQ,���PNQ�ա�OFE,
��PN=OE=4,
���P��������![]() ��
��![]() �������Q�������ǣ�
�������Q�������ǣ�![]() ��
��![]() ����
����
�� ����P��![]() ����·���PN=NM-PM=4 ,
����·���PN=NM-PM=4 ,
�� ![]() ��
��
��֮�ã�![]() ��
��![]() ����ȥ����
����ȥ����
��![]() ��
��
����P��![]() ����Ϸ���ͬ���ɵ�
����Ϸ���ͬ���ɵ�![]() ��
��
����������ĵ�P�ĺ�������![]() ��
��![]() ��
��
����OE�Ĵ�ֱƽ���߽�BE�ڵ�![]() ,��OH��BE�ڵ㣬����BE����
,��OH��BE�ڵ㣬����BE����![]() ���ڵ�H�ĶԳƵ�
���ڵ�H�ĶԳƵ�![]() ,��
,��![]() ,
,
��![]() ��
��![]() ,��
,��![]() ,
,
��![]() ,��
,��![]() (
(![]() ,-2);
,-2);
���![]() �������ǣ�
�������ǣ�![]() ��
��![]() ������
������![]() ���ڵ�S,
���ڵ�S,
��OS=![]() ��
��![]() ����ES=
����ES=![]() ��
��
��![]() =
=![]()
![]()
��![]() ,��
,��![]()
![]()
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�������������������ĵ�F��������(![]() ,-2)����
,-2)����![]() ��
��![]() ��.
��.

 ��������ϵ�д�
��������ϵ�д�