题目内容
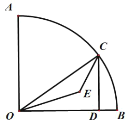
【题目】如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.![]() -1B.
-1B.![]() C.
C.![]() D.2
D.2
【答案】A
【解析】
过点C作CK⊥AB于点K,将线段CK绕点C逆时针旋转90° 得到CH,连接HE,延长HE交AB的延长线于点J;通过证明△CKD≌△CHE (ASA),进而证明所构建的四边形CKJH是正方形,所以当点E与点J重合时,BE的值最小,再通过在Rt△CBK中已知的边角条件,即可求出答案.
如图,过点C作CK⊥AB于点K,将线段CK绕点C逆时针旋转90° 得到CH,连接HE,延长HE交AB的延长线于点J;
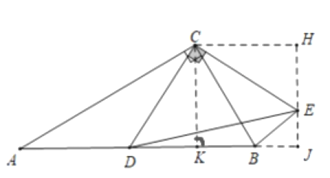
∵将线段CD绕点C逆时针旋转90° ,得到线段CE
∴∠DCE=∠KCH = 90°
∵∠ECH=∠KCH - ∠KCE,∠DCK =∠DCE-∠KCE
∴∠ECH =∠DCK
又∵CD= CE,CK = CH
∴在△CKD和△CHE中
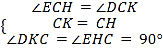
∴△CKD≌△CHE (ASA)
∴∠CKD=∠H=90°,CH=CK
∴∠CKJ =∠KCH =∠H=90°
∴四边形CKJH是正方形
∴CH=HJ=KJ=C'K
∴点E在直线HJ上运动,当点E与点J重合时,BE的值最小
∵∠A= 30°
∴∠ABC=60°
在Rt△CBK中, BC= 2,
∴CK = BCsin60°=![]() ,BK=BCcos60° = 1
,BK=BCcos60° = 1
∴KJ = CK =![]()
所以BJ = KJ-BK=![]() ;
;
BE的最小值为![]() .
.
故选A.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目