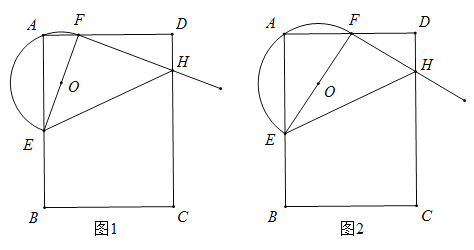
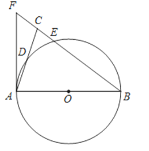
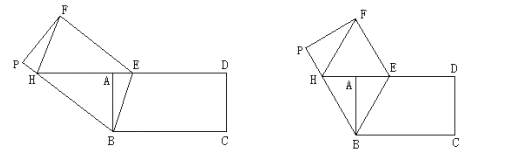
��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y4x4��x�ᣬy��ֱ��ڵ�A��B����A��������yax2bx3a��a0���ϣ�����B����ƽ��3����λ���ȣ��õ���C��
��1�������ߵĶ�������Ϊ ���ú�a�Ĵ���ʽ��ʾ��
��2����a1����t��1��x��tʱ������yax2bx3a��a0�������ֵΪy1����СֵΪy2����y1y22����t��ֵ��
��3�������������߶�BCǡ��һ�������㣬��Ϻ���ͼ����a��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ʱ�����������߶�
ʱ�����������߶�![]() ��һ�����㣮
��һ�����㣮
��������
��1����A��-1��0�����������ߵ�b=-2a���ٽ������߽���ʽ��Ϊ����ʽ������⣻
��2����a=-1ʱ�������߶�������Ϊ��1��4����Ȼ���������������ߵ����ʼ��ɽ��
��3�������B���꣬����B����ƽ��3����λ���ȣ��õ���C�����������ߵĶ���������⣮
�⣺��1��ֱ��y=4x+4��x�ᣬy��ֱ��ڵ�A��B��
��A��-1��0����B��0��4����
��A��������y=ax2+bx-3a��a��0���ϣ�
��b=-2a��
��������y=ax2+bx-3a=a��x-1��2-4a��
�������ߵĶ�������Ϊ��1��-4a����
�ʴ�Ϊ��![]() ��
��
��2����![]() ��
��
�������ߵĽ���ʽΪ![]() ��
��
�ٵ�![]() ʱ��
ʱ��
![]() ��
��
��![]() ��
��
�ڵ�![]() ʱ����
ʱ����![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
�۵�![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
�ܵ�![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
��![]() ��
��![]() ��
��
��3���ٰ�![]() ���������ߣ���
���������ߣ���![]() ��
��
�����������߶�![]() ֻ��һ�������㣬
ֻ��һ�������㣬
��![]() ��
��
��![]() ��
��
�ڵ������߶������߶�![]() ��ʱ��������Ϊ
��ʱ��������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ʱ�����������߶�
ʱ�����������߶�![]() ��һ�����㣮
��һ�����㣮

 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�����Ŀ�� ֣���������ѧΪ�˽�ѧ�������Ķ�����ʱ���������Ӹ��꼶ѧ������������һ����ѧ������ͳ�ƣ���������Դ˴�ͳ���������IJ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ�ش��������⣺
��� | ʱ��Σ�Сʱ�� | Ƶ�� | Ƶ�� |
1 | 0��x��0.5 | 10 | 0.05 |
2 | 0.5��x��1.0 | 20 | 0.10 |
3 | 1.0��x��1.5 | 80 | b |
4 | 1.5��x��2.0 | a | 0.35 |
5 | 2.0��x��2.5 | 12 | 0.06 |
6 | 2.5��x��3.0 | 8 | 0.04 |
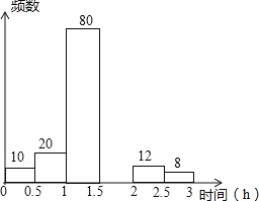
��1������a=______b=______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�ѧ�����Ķ�����ʱ�����λ�����ڵ�______�飻
��4����У����ѧ��3000�ˣ������ѧ�����Ķ���������1.5Сʱ��������
����Ŀ����Ҷ�ǰ���ʡ��Ҫ��������֮һ��2020���²������ڼ䣬ij�賧Ϊ���������棬�����г����飬���²�۸�Ϊ400Ԫ/kg����������������������������x�죨1��x��15����xΪ�������Ʋ�ɱ�������ժ�ͼӹ������Ʋ����������Ϣ���±����ٶ��ò賧ÿ�����������۵��²�û����ʧ�������ڵ���ȫ���۳�����������=�����۶�-���Ʋ�ɱ���
�Ʋ�ɱ���Ԫ/kg�� | 150+10x |
�Ʋ�����kg�� | 40+4x |
��1������ò賧��10������룻
��2����ò賧��x�������Ϊy��Ԫ���������y��x֮��ĺ�����ϵʽ�������y�����ֵ����ʱx��ֵ��