题目内容
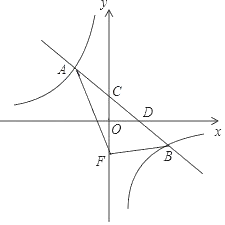
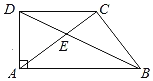
【题目】已知:如图,在梯形ABCD中,CD∥AB,∠DAB=90°,对角线AC、BD相交于点E,AC⊥BC,垂足为点C,且BC2=CECA.
(1)求证:AD=DE;
(2)过点D作AC的垂线,交AC于点F,求证:CE2=AEAF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据相似三角形的判定定理得到△BCE∽△ACB,根据相似三角形的性质得到∠CBE=∠CAB,根据等角的余角相等得到∠BEC=∠DAE,根据等腰三角形的判定定理证明;
(2)根据平行线分线段成比例定理得到![]() ,
,![]() ,得到
,得到![]() ,整理得到CE2=AEEF,根据等腰三角形的三线合一得到AF=EF,证明结论.
,整理得到CE2=AEEF,根据等腰三角形的三线合一得到AF=EF,证明结论.
证明:(1)∵BC2=CECA,
∴![]() ,又∠ECB=∠BCA,
,又∠ECB=∠BCA,
∴△BCE∽△ACB,
∴∠CBE=∠CAB,
∵AC⊥BC,∠DAB=90°,
∴∠BEC+∠CBE=90°,∠DAE+∠CAB=90°,
∴∠BEC=∠DAE,
∵∠BEC=∠DEA,
∴∠DAE=∠DEA,
∴AD=DE;
(2)过点D作AC的垂线,交AC于点F,如图,
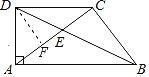
∵DF⊥AC,AC⊥BC,
∴∠DFE=∠BCA=90°,
∴DF∥BC,
∴![]() ,
,
∵DC∥AB,
∴![]() ,
,
∴![]() ,
,
∴CE2=AEEF,
∵AD=DE,DF⊥AC,
∴AF=EF,
∴CE2=AEAF.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目