Question

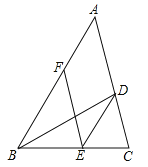
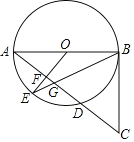
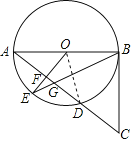
【题目】如图，在⊙O中，AB是⊙O的直径，F是弦AD的中点，连结OF并延长OF交⊙O于点E，连结BE交AD于点G，延长AD至点C，使得GC＝BC，连结BC．

（1）求证：BC是⊙O的切线．

（2）⊙O的半径为10，sinA＝，求EG的长．

Answer 1

【答案】（1）见解析；（2）2

【解析】

(1)连结OD，求出∠ABE+∠GBC=90°，根据切线的判定得出即可；
(2)解直角三角形求出AF、OF，证明，求出BC和AC，进而求出EF、FG，根据勾股定理可得EG的长．

(1)证明：连结OD，

∵OA=OD，F是弦AD的中点，

∴OF⊥AD，

∴∠EFG=90°，

∴∠E+∠FGE=90°，

∵BC=GC，

∴∠BGC=∠GBC，

∵∠FGE=∠BGC，

∴∠GBC=∠FGE，

∵OE=OB，

∴∠ABE=∠E，

∴∠ABE+∠GBC=90°，

∴∠ABC=90°，

∴BC是⊙O的切线；

(2)∵sinA=，OA=10，

∴OF=OA·sinA=6，

∴，

∵∠OAF=∠CAB，∠OFA=∠CBA=90°，

∴，

∴，即，

∴BC=GC=15，

∴AC==25，

∴AG=AC-GC=10，EF=OE-OF=10-6=4，

∴FG=2，

在中，∠EFG=90°，FG=2，EF=4，

∴．