Question

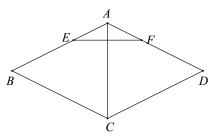
【题目】四边形ABCD中，AB＝BC＝CD，∠ABC＝60°，点E在AB上，∠AED＝∠CEB，AD＝5，DE+CE＝，则BD的长为_____．

Answer 1

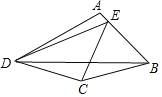
【答案】7

【解析】

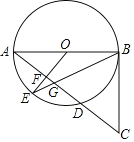
连接AC，延长DE至F，使EF=CE，作正三角形ADG，使B、G分别在AD两侧，连接AF、BF、BG，证明△BEF≌△BEC(SAS)，可证得△ABF是等边三角形，得出AF=AB，∠BAF=60°，证明△DAF≌△GAB(SAS)，得出BG=DF=DE+EF=DE+CE=，证明△ABC是等边三角形，得出AC=BC=DC，∠ACB=60°，得出点C是△ABD的外心，由圆周角定理得出∠ADB=∠ACB=30°，证出∠BDG=∠ADB+∠ADG=90°，由勾股定理即可得出答案．

连接AC，延长DE至F，使EF=CE，作正三角形ADG，使B、G分别在AD两侧，连接AF、BF、BG，如图所示：

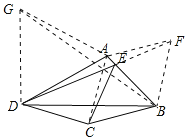
∵∠AED=∠CEB，∠BEF=∠AED，

∴∠BEF=∠AED=∠CEB，

在△BEF和△BEC中，，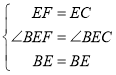

∴△BEF≌△BEC(SAS)，

∴∠ABF=∠ABC=60°，BF=BC=AB，

∴△ABF是等边三角形，

∴AF=AB，∠BAF=60°，

∵△ADG是等边三角形，

∴∠ADG=∠DAG=60°=∠BAF，AG=AD=5，

∴∠DAF=∠DAB+∠BAF=∠DAB+∠DAG=∠GAB，

在△DAF和△GAB中，，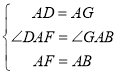

∴△DAF≌△GAB(SAS)，

∴BG=DF=DE+EF=DE+CE=，

∵AB=BC，∠ABC=60°，

∴△ABC是等边三角形，

∴AC=BC=DC，∠ACB=60°，

∴点C是△ABD的外心，

∴∠ADB=∠ACB=30°，

∴∠BDG=∠ADB+∠ADG=90°，

∴BD=；

故答案为：7．