题目内容
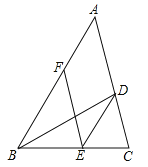
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)已知BD是△ABC的角平分线,根据角平分线的定义可得∠ABD=∠DBE;再由DE∥AB,根据两直线平行,内错角相等可得∠ABD=∠BDE,所有∠DBE=∠BDE,根据等腰三角形的性质可得BE=DE;再由BE=AF,可得AF=DE;根据一组对边平行且相等的四边形即可判定四边形ADEF是平行四边形;(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,易求得DG与DE的长,继而求得答案.
试题解析:
(1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE;
∵BE=AF,
∴AF=DE;
∴四边形ADEF是平行四边形;
(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,
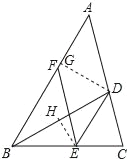
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠ABD=∠EBD=30°,
∴DG=![]() BD=
BD=![]() ×4=2,
×4=2,
∵BE=DE,
∴BH=DH=2,
∴BE=![]() =
=![]() ,
,
∴DE=![]() ,
,
∴四边形ADEF的面积为:DEDG=![]() .
.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目