题目内容
【题目】问题发现：
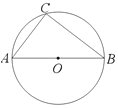
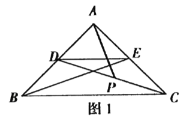
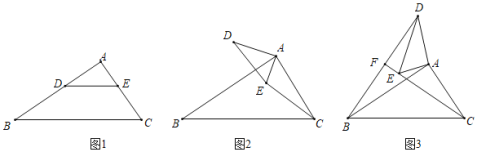
(1)如图1，在Rt△ABC中，∠A＝90°，AB＝kAC(k＞1)，D是AB上一点，DE∥BC，则BD，EC的数量关系为 ．
类比探究
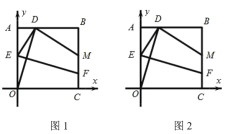
(2)如图2，将△AED绕着点A顺时针旋转，旋转角为a(0°＜a＜90°)，连接CE，BD，请问(1)中BD，EC的数量关系还成立吗？说明理由
拓展延伸：
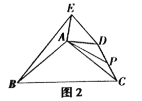
(3)如图3，在(2)的条件下，将△AED绕点A继续旋转，旋转角为a(a＞90°)．直线BD，CE交于F点，若AC＝1，AB＝
，则当∠ACE＝15°时，BFCF的值为_____．
【答案】(1)BD＝kEC；(2)成立，理由见解析；(3)1或2.
【解析】
问题发现：（1）由平行线分线段成比例可得
，即可得BD＝kEC；
类比探究：（2）通过证明△ABD∽△ACE，可得
＝k，即可得BD＝kEC；
拓展延伸：（3）分两种情况讨论，由相似三角形的性质可得∠ACE＝∠ABD，即可证∠BFC＝90°，由直角三角形的性质和勾股定理可求BFCF的值．
问题发现：
(1)∵DE∥BC，
∴，
∵AB＝kAC，
∴BD＝kEC，
故答案为：BD＝kEC；
类比探究：
(2)成立，
理由如下：连接BD
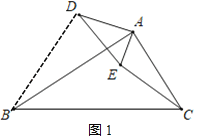
由旋转的性质可知，∠BAD＝∠CAE
∵
，
∴△ABD∽△ACE，
∴＝k，
故BD＝kEC；
拓展延伸：
(3)BFCF的值为2或1；
由旋转的性质可知∠BAD＝∠CAE
∵，
∴△ABD∽△ACE
∴∠ACE＝15°＝∠ABD
∵∠ABC+∠ACB＝90°
∴∠FBC+∠FCB＝90°
∴∠BFC＝90°
∵∠BAC＝90°，AC＝1，AB＝
，
∴tan∠ABC＝
，
∴∠ABC＝30°
∴∠ACB＝60°
分两种情况
①如图2，
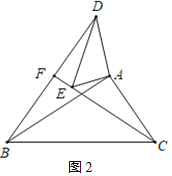
∴在Rt△BAC中，∠ABC＝30°，AC＝1，
∴BC＝2AC＝2，
∵在Rt△BFC中，∠CBF＝30°+15°＝45°，BC＝2
∴BF＝CF＝
∴BFCF＝()2＝2
②如图3，
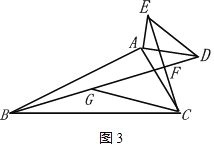
设CF＝a，在BF上取点G，使∠BCG＝15°
∵∠BCF＝60°+15°＝75°，∠CBF＝∠/span>ABC﹣∠ABD＝30°﹣15°＝15°，
∴∠CFB＝90°
∴∠GCF＝60°
∴CG＝BG＝2a，GF＝a．
∵CF2+BF2＝BC2
∴a2+(2a+a） 2＝22，
解得a2＝2﹣，
∴BFCF＝(2+)aa＝(2+)a2＝1，
即：BFCF＝1或2．
故答案为：1或2．
