题目内容
【题目】图1、图2分别是8×8的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
(1)在图1中画一个以线段AB为一边的正方形,并求出此正方形的面积;(所画正方形各顶点必须在小正方形的顶点上)
(2)在图2中画一个以线段AB为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为12.
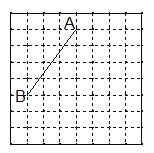

图1 图2 备用图
【答案】(1)图见解析;此正方形的面积为25;(2)图见解析.
【解析】
(1)根据正方形的性质作图,利用勾股定理求出AB即可得到面积;
(2)根据等腰三角形的性质和三角形的面积为12作图即可.
解:(1)如图所示:正方形ABCD即为所求,
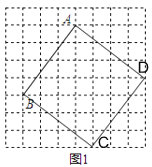
由勾股定理可知AB=![]() ,
,
∴此正方形的面积=AB2=25;
(2)如图所示:△ABC即为所求.


练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目