Question

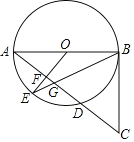
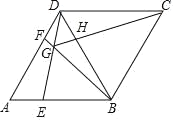
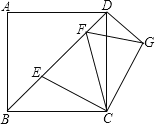
【题目】如图，在正方形ABCD中，AB＝a，点E，F在对角线BD上，且∠ECF＝∠ABD，将△BCE绕点C旋转一定角度后，得到△DCG，连接FG．则下列结论：

①∠FCG＝∠CDG；

②△CEF的面积等于；

③FC平分∠BFG；

④BE2+DF2＝EF2；

其中正确的结论是_____．（填写所有正确结论的序号）

Answer 1

【答案】①③④

【解析】

由正方形的性质可得AB＝BC＝CD＝AD＝a，∠ABD＝∠CBD＝∠ADB＝∠BDC＝45°，由旋转的性质可得∠CBE＝∠CDG＝45°，BE＝DG，CE＝CG，∠DCG＝∠BCE，由SAS可证△ECF≌△GCF，可得EF＝FG，∠EFC＝∠GFC，S△ECF＝S△CFG，即可求解．

解：∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD＝a，∠ABD＝∠CBD＝∠ADB＝∠BDC＝45°，

∴∠ECF＝∠ABD＝45°，

∴∠BCE+∠FCD＝45°，

∵将△BCE绕点C旋转一定角度后，得到△DCG，

∴∠CBE＝∠CDG＝45°，BE＝DG，CE＝CG，∠DCG＝∠BCE，

∴∠FCG＝∠ECF＝45°，

∴∠FCG＝∠CDG＝45°，故①正确，

∵EC＝CG，∠FCG＝∠ECF，FC＝FC，

∴△ECF≌△GCF（SAS）

∴EF＝FG，∠EFC＝∠GFC，S△ECF＝S△CFG，

∴CF平分∠BFG，故③正确，

∵∠BDG＝∠BDC+∠CDG＝90°，

∴DG2+DF2＝FG2，

∴BE2+DF2＝EF2，故④正确，

∵DF+DG＞FG，

∴BE+DF＞EF，

∴S△CEF＜S△BEC+S△DFC，

∴△CEF的面积＜S△BCD＝，故②错误；

故答案为：①③④