题目内容
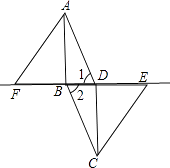
【题目】如图，AB∥CD，AC∥BE，∠MAC=40，∠D=50°，CH平分∠ACD，BH平分∠ABD，
（1）求∠EBH的角度
（2）求∠BHC的角度
【答案】（1）25°；（2）135°
【解析】
（1）根据平行线的性质得出∠MBE，根据角平分线的定义结合∠D得出∠ABH，通过∠EBH=∠ABH-∠MBE得出结果；
（2）延长CH交BD于点O，根据三角形外角得出∠BHC=∠OBH+∠BOH，∠BOH=∠D+∠HCD，求出∠HCD，结合已知条件即可得出结果.
解：（1）∵AB∥CD，
∴∠ABD+∠D=180°，
∵∠D=50°，
∴∠ABD=130°，
∵BH平分∠ABD，
∴∠ABH=∠DBH=65°，
∵AC∥BE，
∴∠MAC=∠MBE=40°，
∴∠EBH=∠ABH-∠MBE=65°-40°=25°；
（2）延长CH交BD于点O，
∵∠BHC=∠OBH+∠BOH，
∠BOH=∠D+∠HCD，
∵AB∥CD，
∴∠MAC=∠ACD=40°，
∵CH平分∠ACD，
∴∠HCD=20°，
∴∠BOH=∠D+∠HCD=70°，
∠BHC=∠OBH+∠BOH=65°+70°=135°.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】点燃一根蜡烛后，蜡烛的高度h（厘米）与燃烧时间t（分）之间的关系如下表：
t/分 | 0 | 2 | 4 | 6 | 8 | 10 |
h/厘米 | 30 | 29 | 28 | 27 | 26 | 25 |
写出蜡烛的高度h（厘米）与燃烧时间t（分）之间的关系式_____；这根蜡烛最多能燃烧的时间为_____分．
