Question

【题目】已知A，B两点在直线m上，C，D两点在直线n上，∠BAD=α，∠BCD=β．

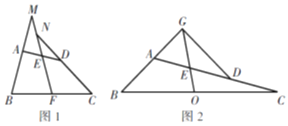
（1）如图1，若∠BAD=∠ADC，求证∠ABC=∠BCD．

（2）如图2，m∥n，过点D作DE⊥BC于点E，∠BAD与∠DEB的角平分线相交于点P，求∠P（用α，β的式子表示）

（3）在（2）的条件下，若点A沿直线m向右运动，且不与B点重合，则∠APE=　（用α，β的式子表示，不写证明过程）．

Answer 1

【答案】（1）见解析；（2）∠P=α+β-45°；（3）α+β-45°或135°+β-α

【解析】

（1）利用平行线的判定和性质即可证明；

（2）根据条件求出∠DEP=45°，∠BAP=∠PAD=α，设AP，BC交于N，推出∠ANC=∠BAP+∠ABC=∠P+∠BEP，从而得到∠P的度数；

（3）分点A在点B左侧，点A在点B右侧两种情况，参照（2）中过程，分别求出∠APE的度数即可.

解：（1）∵∠BAD=∠ADC，

∴m∥n，

∴∠ABC=∠BCD；

（2）∵DE⊥BC，

∴∠DEC=∠DEB=90°，

∵∠BAD与∠DEB的角平分线相交于点P，

∴∠DEP=∠BEP=∠DEB=45°，

∠BAP=∠PAD=∠BAD=α，

∵m∥n，

∴∠ABC=∠BCD=β，

设AP，BC交于N，

∵∠ANC=∠BAP+∠ABC=∠P+∠BEP，

∴α+β=∠P+45°，

∴∠P=α+β-45°；

（3）若点A在点B左侧，由（2）得：

∠APE=α+β-45°；

若点A在点B右侧，延长EP，交AD于Q，

∴∠APE=∠PAQ+∠AQP，

∵AP平分∠BAD，

∴∠PAQ=α，

由（2）得∠BEP=∠DEP=45°，

∴∠AQP=∠DEP+∠ADE=45°+∠ADE，

而∠EDC=90°-∠BCD=90°-β，

∴∠ADE=180°-（90°-β）-α=90°+β-α，

∴∠AQP=45°+90°+β-α，

∴∠APE=∠PAQ+∠AQP=α+45°+90°+β-α=135°+β-α.