题目内容
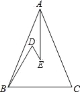
【题目】在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=![]()

求:(1)求AD的长;
(2)△ABC是直角三角形吗?为什么?
【答案】(1)![]() ;(2)△ABC为直角三角形
;(2)△ABC为直角三角形
【解析】试题分析:(1)由CD垂直于AB,得到三角形BCD与三角形ACD都为直角三角形,由BC与DB,利用勾股定理求出CD的长,再利用勾股定理求出AD的长即可;
(2)三角形ABC为直角三角形,理由为:由BD+AD求出AB的长,利用勾股定理的逆定理得到三角形ABC为直角三角形.
解:(1)∵CD⊥AB,
∴∠CDB=∠CDA=90°,
在Rt△BCD中,BC=3,DB=,
根据勾股定理得:CD=![]() =
=![]() ,
,
在Rt△ACD中,AC=4,CD=![]() ,
,
根据勾股定理得:AD=![]() =
=![]() ;
;
(2)△ABC为直角三角形,理由为:
∵AB=BD+AD=+![]() =5,
=5,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目