题目内容
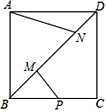
【题目】如图，正方形ABCD的对角线上的两个动点M、N，满足AB=
MN，点P是BC的中点，连接AN、PM，若AB=6，则当AN+PM取最小值时，线段AN的长度为（ ）
A.4B.2
C.6D.3
【答案】B
【解析】
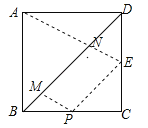
过P作PE∥BD交CD于E，连接AE交BD于N，过P作PM∥AE交BD于M，此时，AN+PM的值最小，根据三角形的中位线的性质得到PE=
BD，根据平行四边形的性质得到EN=PM，根据勾股定理得到AE=
=3
，根据相似三角形的性质即可得到结论．
过P作PE∥BD交CD于E，连接AE交BD于N，过P作PM∥AE交BD于M，此时，AN+PM的值最小．
∵P是BC的中点，∴E为CD的中点，∴PE=BD．
∵AB=
BD，AB=
MN，∴MN=BD，∴PE=MN，∴四边形PENM是平行四边形，∴EN=PM．
∵AE==3．
∵AB∥CD，∴△ABN∽△EDN，∴
=
=2，∴AN=2．
故选B．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
