Question

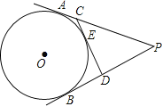
【题目】如图，BE是⊙O的直径，半径OA⊥弦BC，垂足为D，连接AE、EC．

（1）若∠AEC＝25°，求∠AOB的度数；

（2）若∠A＝∠B，EC＝4，求⊙O的半径．

Answer 1

【答案】（1）∠AOB＝50°；（2）⊙O的半径为4．

【解析】

（1）连接OC，根据垂径定理可得，根据圆周角定理即可求出∠AOB的度数；（2）由BE是直径可得∠ECB=90°，可得EC//OA，根据平行线的性质可得∠A=∠AEC，根据等腰三角形的性质可得∠A=∠OEA，由∠A=∠B即可证明∠B＝∠AEB＝∠AEC，可得∠B=30°，根据含30°角的直角三角形的性质即可得答案.

（1）连接OC．

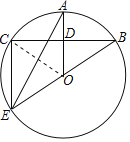
∵半径OA⊥弦BC，

∴，

∴∠AOC＝∠AOB，

∵∠AOC＝2∠AEC＝50°，

∴∠AOB＝50°．

（2）∵BE是⊙O的直径，

∴∠ECB＝90°，

∴EC⊥BC，

∵OA⊥BC，

∴EC∥OA，

∴∠A＝∠AEC，

∵OA＝OE，

∴∠A＝∠OEA，

∵∠A＝∠B，

∴∠B＝∠AEB＝∠AEC，

∵∠B+∠AEB+∠AEC=90°，

∴∠B=30°，

∵EC＝4，

∴EB＝2EC＝8，

∴⊙O的半径为4．