题目内容
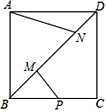
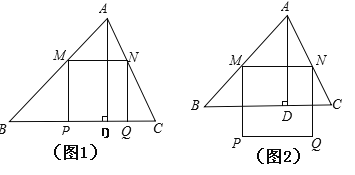
【题目】锐角△ABC中,BC=6,![]() ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1)求△ABC中边BC上高AD;
(2)当x为何值时,PQ恰好落在边BC上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
【答案】(1)4;(2)2.4(或![]() );(3)3,6.
);(3)3,6.
【解析】
(1)利用三角形的面积公式容易得出△ABC中边BC上高AD的长度.
(2)因为正方形的位置在变化,但是△AMN∽△ABC没有改变,利用相似三角形对应边上高的比等于相似比,得出等量关系,代入解析式可得出;
(3)用含x的式子表示矩形MEFN边长,从而求出面积的表达式,配方成顶点式可得解.
解:(1)由BC=6,S△ABC=12,得AD=4;
(2)当PQ恰好落在边BC上时,
∵MN∥BC,
∴△AMN∽△ABC.
![]()
即![]() ;
;
(3)设BC分别交MP,NQ于E,F,则四边形MEFN为矩形.
设ME=NF=h,AD交MN于G(如图2)GD=NF=h,AG=4-h.
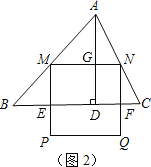
∵MN∥BC,
∴△AMN∽△ABC.
![]() 即
即![]() ,
,
![]() ,
,
![]() ,
,
配方得:![]()
∴当x=3时,y有最大值,最大值是6.

练习册系列答案
相关题目