题目内容
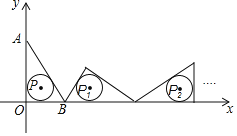
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),且过点
与x轴交于A,B两点(点A在点B的左侧),且过点![]() .
.
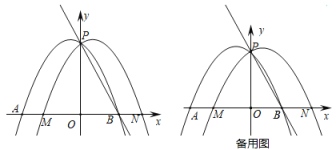
(1)直接写出a的值和点B的坐标;
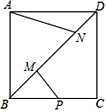
(2)将抛物线向右平移2个单位长度,所得的新抛物线与x轴交于M,N两点,两抛物线交于点P,求点M到直线PB的距离;
(3)在(2)的条件下,若点D为直线BP上的一个动点,是否存在点D,使得![]() ?若存在,请求出点D的坐标:若不存在,请说明理由.
?若存在,请求出点D的坐标:若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)D点坐标为
;(3)D点坐标为![]() 或
或![]() .
.
【解析】
(1)将点(-2,4)代入y=a(x+5)(x3)即可求出a,根据抛物线解析式可直接得出点B的坐标;
(2)作![]() 于点C,连接MP,首先求出平移后的新抛物线解析式,得到点M、P的坐标,然后求出BP,利用S△PMB=
于点C,连接MP,首先求出平移后的新抛物线解析式,得到点M、P的坐标,然后求出BP,利用S△PMB=![]() ×PB×MC=
×PB×MC=![]() ×MB×OP,即可求解;
×MB×OP,即可求解;
(3)作BE平分![]() 交OP于E,作
交OP于E,作![]() 于F,根据
于F,根据![]() 求出
求出![]() ,然后在
,然后在![]() 中,可得
中,可得![]() ,然后分情况讨论:①点D在x轴上方,设AD交y轴于点H,根据
,然后分情况讨论:①点D在x轴上方,设AD交y轴于点H,根据![]() 求出点H的坐标,然后求得直线PB与直线AH的解析式,联立即可求出点D的坐标,②点D在x轴下方,设AD交y轴于点K,同理可求点D的另一个坐标.
求出点H的坐标,然后求得直线PB与直线AH的解析式,联立即可求出点D的坐标,②点D在x轴下方,设AD交y轴于点K,同理可求点D的另一个坐标.
解:(1)将点![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∵抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),
与x轴交于A,B两点(点A在点B的左侧),
∴![]() ;
;
(2)作![]() 于点C,连接MP,
于点C,连接MP,
由题意得:将点![]() 向右平移2个单位得到点M为
向右平移2个单位得到点M为![]() ,
,
原抛物线解析式为![]() ,
,
则新抛物线解析式为![]() ,
,
联立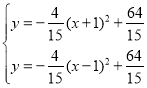 ,解得:
,解得:![]() ,
,
∴点P的坐标为![]() ,
,
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵S△PMB=![]() ×PB×MC=
×PB×MC=![]() ×MB×OP,
×MB×OP,
∴![]() ,
,
即点M到直线PB的距离为![]() ;
;
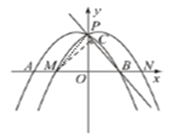
(3)存在符合题意的点D为![]() 或
或![]() ,
,
作BE平分![]() 交OP于E,作
交OP于E,作![]() 于F,
于F,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴在![]() 中,
中,![]() ,
,
分两种情况:
①如图,点D在x轴上方,设AD交y轴于点H,
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]() ,
,
∴点H坐标为![]() ,
,
设直线PB的解析式为![]() ,
,
代入![]() 和
和![]() 得:
得:![]() ,解得:
,解得: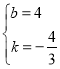 ,
,
∴直线PB的解析式为![]() ,
,
设直线AH的解析式为![]() ,
,
代入![]() 和
和![]() 得:
得: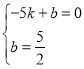 ,解得:
,解得:![]() ,
,
∴直线AH的解析式为![]() ,
,
联立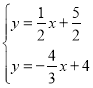 ,得
,得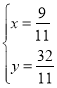 ,
,
∴直线AH与直线BP的交点坐标为![]() ;
;
②如图,点D在x轴下方,设AD交y轴于点K,
同①的方法可求得点D坐标为![]() ,
,
综上所述,存在满足题目条件的D点坐标为![]() 或
或![]() .
.

【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值