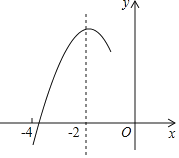题目内容
【题目】如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式;
(2)点D为y轴右侧抛物线上一点,是否存在点D,使S△ABC=S△ABD?若存在,请求出点D坐标:若不存在,请说明理由.
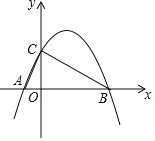
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)存在,D(3,2)或D(
x+2;(2)存在,D(3,2)或D(![]() ,2).
,2).
【解析】
(1)把A、B点代入抛物线y=ax2+bx+2得到关于a、b的方程组,解方程组求出a、b得到抛物线解析式;
(2)先确定C(0,2),设D(x,![]() x2
x2![]() x+2)(x>0),利用三角形面积公式得到
x+2)(x>0),利用三角形面积公式得到![]() (4+1)×|
(4+1)×|![]() x2
x2![]() x+2|
x+2|![]() (4+1)×2,然后分别解方程
(4+1)×2,然后分别解方程![]() x2
x2![]() x+2=2和
x+2=2和![]() x2
x2![]() x+2=﹣2,从而得到满足条件的D点坐标.
x+2=﹣2,从而得到满足条件的D点坐标.
(1)∵抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),∴![]() ,
,
解得: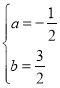 ,∴抛物线解析式为y
,∴抛物线解析式为y![]() x2
x2![]() x+2;
x+2;
(2)存在点D,使S△ABC=S△ABD.
当x=0时,y![]() x2
x2![]() x+2=2,则C(0,2),
x+2=2,则C(0,2),
设D(x,![]() x2
x2![]() x+2)(x>0),
x+2)(x>0),
![]() (4+1)×|
(4+1)×|![]() x2
x2![]() x+2|
x+2|![]() (4+1)×2,
(4+1)×2,
当![]() x2
x2![]() x+2=2时,解得:x1=0(舍去),x2=3,此时D(3,2);
x+2=2时,解得:x1=0(舍去),x2=3,此时D(3,2);
当![]() x2
x2![]() x+2=﹣2时,解得:x1
x+2=﹣2时,解得:x1![]() (舍去),x2
(舍去),x2![]() ,此时D(
,此时D(![]() ,2).
,2).

 阅读快车系列答案
阅读快车系列答案【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值