题目内容
已知抛物线y=x2-2x+a与直线y=x+1有两个公共点A(x1,y1),B(x2,y2),且x2>x1≥0.
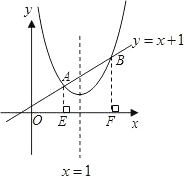
(1)求抛物线的对称轴,并在所给坐标系中画出对称轴和直线y=x+1;
(2)试求a的取值范围;
(3)若AE⊥x,E为垂足,BF⊥x轴,F为垂足,试求S梯形ABFE的最大值.

(1)求抛物线的对称轴,并在所给坐标系中画出对称轴和直线y=x+1;
(2)试求a的取值范围;
(3)若AE⊥x,E为垂足,BF⊥x轴,F为垂足,试求S梯形ABFE的最大值.

(1)对称轴x=1,
(2)方程组
消去y,
得x2-3x+a-1=0.
由题意可知x1,x2是方程x2-3x+a-1=0的两个不相等的根,
∴x1+x2=3,x1•x2=a-1,
∵x2>x1≥0,
∴x1•x2≥0,
得a-1≥0,a≥1,
又△=13-4a>0,
∴a<
,
故1≤a<
.
(3)∵点A,B在直线y=x+1上,
∴y1=x1+1,y2=x2+1,
∴S梯形ABFE=
(AE+BF)×EF,
=
(y1+y2)(x2-x1)=
(x1+x2+2)
=
∵1≤a<
,
∴a=1时,S梯形ABFE取最大值
.
(2)方程组
|
得x2-3x+a-1=0.
由题意可知x1,x2是方程x2-3x+a-1=0的两个不相等的根,
∴x1+x2=3,x1•x2=a-1,
∵x2>x1≥0,
∴x1•x2≥0,
得a-1≥0,a≥1,
又△=13-4a>0,
∴a<
| 13 |
| 4 |
故1≤a<
| 13 |
| 4 |
(3)∵点A,B在直线y=x+1上,
∴y1=x1+1,y2=x2+1,
∴S梯形ABFE=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| 5 |
| 2 |
| 13-4a |
∵1≤a<
| 13 |
| 4 |
∴a=1时,S梯形ABFE取最大值
| 15 |
| 2 |


练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目


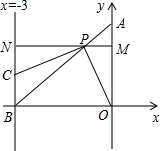 角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.
角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由. 标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.
标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.