题目内容
二次函数图象过A、B、C三点，点A（-l，0），B（3，0），点C在y轴负半轴上，且OB=OC．
（1）求这个二次函数的解析式：
（2）将该二次函数图象向右平移几个单位，可使平移后所得图象过点（1，5），并求出平移后图象与y轴的交点坐标．
（1）求这个二次函数的解析式：
（2）将该二次函数图象向右平移几个单位，可使平移后所得图象过点（1，5），并求出平移后图象与y轴的交点坐标．
（1）由题知，C（0，-3），
∴设二次函数的解析式为y=a（x+1）（x-3），
将（0，-3）代入，得a（0-3）=-3，
解得a=1，
∴二次函数的解析式为y=（x+1）（x-3）；
（2）设二次函数图象向右平移h个单位，可使平移后所得图象过点（1，5），
得平移后的解析式为y=（x-1-h）2-4，
将（1，5）代入，得（1-1-h）2-4=5，
解得h=±3，
∵h＞0，
∴h=3，
∴向右平移3个单位，可使平移后所得图象过点（1，5），
令x=0，得（0-1-3）2-4=12，
∴与y轴的交点坐标为（0，12）．
∴设二次函数的解析式为y=a（x+1）（x-3），
将（0，-3）代入，得a（0-3）=-3，
解得a=1，
∴二次函数的解析式为y=（x+1）（x-3）；
（2）设二次函数图象向右平移h个单位，可使平移后所得图象过点（1，5），
得平移后的解析式为y=（x-1-h）2-4，
将（1，5）代入，得（1-1-h）2-4=5，
解得h=±3，
∵h＞0，
∴h=3，
∴向右平移3个单位，可使平移后所得图象过点（1，5），
令x=0，得（0-1-3）2-4=12，
∴与y轴的交点坐标为（0，12）．
练习册系列答案
相关题目
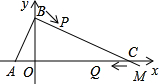、Q、C为顶点的三角形是等腰三角形．（点P到点C时停止运动，点Q也同时停止运动），求t的值．
点B，tan∠ABO=
